Advertisements
Advertisements
प्रश्न
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
उत्तर
v = vm sin ωt
Let the current in the circuit be led the applied voltage by an angleΦ.
`i= i_m sin(omegat +phi)`
The Kirchhoff’s voltage law gives`L ((di)/dt +Ri +q/C = v)`.
It is given that v = vm sin ωt (applied voltage)
`L(d^2q)/(dt^2) +R(dq)/(dt) +q/C = v_m sinomegat ...... (1)`
On solving the equation, we obtain
`q = q_m sin(omegat + theta)`
`(dp)/(dt) = q_momega cos(omegat +theta)`
`((d^2)q)/(dt^2) = -q_momega^2 sin(omegat +theta)`
On substituting these values in equation (1), we obtain
`q_momega[R cos(omegat +theta)+ (X_c -X_L)sin(omegat +theta)] = v_msinomegat`
`X_c = 1/(omegaC) X_c = omegaL`
`Z = sqrt(R^2 +(X_c - X_L)^2`
`q_momegaZ[R/Z cos(omegat+theta)+((X_c -X_L))/Z sin (omegat+theta)] = v_m sin omegat ........... (2)`
Let `cos phi = R/2` and `(X_c -X_L)/Z = sinphi`
This gives
`tan phi = (X_c - X_L)/R`
On substituting this in equation (2), we obtain
`q_momegaZcos (omegat +theta -phi) = v_msinomegat`
On comparing the two sides, we obtain
`V_m = q_momegaZ = i+mZ`
`i_m = q_momega`
and `(theta-phi) = -pi/2`
`I = (dp)/(dt ) =q_momega cos (omegat+theta)`
`=i_m cos(omegat+theta)`
Or
`i = i_m sin(omegat +theta)`
Where,`i_m = (v_m)/Z = (v_m)/(sqrt(R^2 +(X_c - X_L)^2)`
And
`phi = tan^-1((X_c -X_L)/R)`
The condition for resonance to occur
`i_m = v_m/sqrt(R^2 +(X_C - X_L)^2)`
For resonance to occur, the value of im has to be the maximum.
The value of im will be the maximum when
`X_c = X_L`
`1/(omega C) = omegaL`
`omega^2 = 1/(LC)`
`omega = 1/(sqrtLC)`
`2pif = 1/sqrt(LC)`
`f = 1/(02pisqrt(LC)`
Power factor = cos Φ
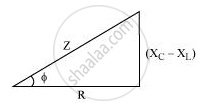
Where,`cosphi = R/Z = R/(sqrt(R^2 +(X_c- X_L)^2)`
(i) Conditions for maximum power factor (i.e., cos Φ = 1)
-
XC = XL
Or
-
R = 0
(ii) Conditions for minimum power factor
-
When the circuit is purely inductive
-
When the circuit is purely capacitive
APPEARS IN
संबंधित प्रश्न
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
In a series LCR circuit, obtain the condition under which the impedance of the circuit is minimum ?
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit. Plot a graph to show the variation of current with frequency of the source, explaining the nature of its variation.
The time constant of an LR circuit is 40 ms. The circuit is connected at t = 0 and the steady-state current is found to be 2.0 A. Find the current at (a) t = 10 ms (b) t = 20 ms, (c) t = 100 ms and (d) t = 1 s.
An LR circuit with emf ε is connected at t = 0. (a) Find the charge Q which flows through the battery during 0 to t. (b) Calculate the work done by the battery during this period. (c) Find the heat developed during this period. (d) Find the magnetic field energy stored in the circuit at time t. (e) Verify that the results in the three parts above are consistent with energy conservation.
In a series, LCR circuit, obtain an expression for the resonant frequency,
Use the expression for Lorentz force acting on the charge carriers of a conductor to obtain the expression for the induced emf across the conductor of length l moving with velocity v through a magnetic field B acting perpendicular to its length.
Using the phasor diagram, derive the expression for the current flowing in an ideal inductor connected to an a.c. source of voltage, v= vo sin ωt. Hence plot graphs showing the variation of (i) applied voltage and (ii) the current as a function of ωt.
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
For a series LCR-circuit, the power loss at resonance is ______.
