Advertisements
Advertisements
प्रश्न
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit. Plot a graph to show the variation of current with frequency of the source, explaining the nature of its variation.
Advertisements
उत्तर
Let an alternating Emf E = E0 sinωt is applied to a series combination of inductor L, capacitor C and resistance R. Since all three of them are connected in series the current through them is same. But the voltage across each element has a different phase relation with current.
The potential difference VL, VC and VR across L, C and R at any instant is given by
VL = IXL, VC = IXC and VR = IR
Where I is the current at that instant.
XL is inductive reactance and
XC is capacitive reactance.
VR is in phase with I. VL leads I by 90° and VC lags behind I by 90°
In the phases diagram,
VL and VC are opposite to each other. If VL > VC then resultant (VL − VC) is represent by OD. OR represent the resultant of VR and (VL − VC). It is equal to the applied Emf E.
`E^2 = V_R^2 + (V_L -V_C)^2`
`E^2 =I^2 +[R^2+(X_L -X_c)^2]`
`or I =E/sqrt (R^2 + (X_2 -X_c)^2)`
The term `sqrt(R^2 +(X_2 - X_c))` is called impedance Z of the LCR circuit.
`Z = sqrt(R^2 +(X_2 -X_c)^2) =sqrt(R^2 +(L omega-1/(comega))^2)`
Emf leads current by a phase angle Φ
`tan phi = (V_L -V_C)/R = (X_L - X_c)/R =(Lomega -1/(comega))/R`
When resonance takes place
`omegaL= 1/(omegac)`
Impedance of circuit becomes equal to R. Current becomes maximum and is equal to `E/R`
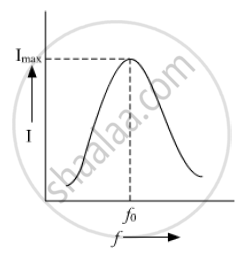
`omega_0 = 1/sqrt(LC)`
`f_0 = omega_0/(2pi) = 1/(2pisqrt(LC))`
This is the condition for resonance.
When at resonance f = f0 the current in the circuit is maximum and hence impedance of the circuit is maximum for values of f less than or greater than f0 comparatively small current flames in the circuit.
संबंधित प्रश्न
Define 'quality factor' of resonance in a series LCR circuit. What is its SI unit?
Two coils A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10 Ω. Each coil is connected to an ideal battery of emf 2.0 V at t = 0. Let iA and iBbe the currents in the two circuit at time t. Find the ratio iA / iB at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1 s.
Assertion: When the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero, and so there is no current through the inductor or the capacitor.
Reason: The net current in the inductor and capacitor is zero.
A series LCR circuit containing a 5.0 H inductor, 80 µF capacitors, and 40 Ω resistor is connected to a 230 V variable frequency ac source. The angular frequencies of the source at which power is transferred to the circuit are half the power at the resonant angular frequency are likely to be ______.
A series LCR circuit containing 5.0 H inductor, 80 µF capacitor and 40 Ω resistor is connected to 230 V variable frequency ac source. The angular frequencies of the source at which power transferred to the circuit is half the power at the resonant angular frequency are likely to be ______.
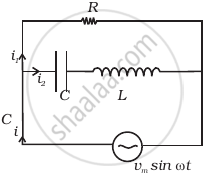
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
A series LCR circuit driven by 300 V at a frequency of 50 Hz contains a resistance R = 3 kΩ, an inductor of inductive reactance XL = 250 πΩ, and an unknown capacitor. The value of capacitance to maximize the average power should be ______.
A series RL circuit with R = 10 Ω and L = `(100/pi)` mH is connected to an ac source of voltage V = 141 sin (100 πt), where V is in volts and t is in seconds. Calculate
- the impedance of the circuit
- phase angle, and
- the voltage drop across the inductor.
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit.
