Advertisements
Advertisements
प्रश्न
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit. Plot a graph to show the variation of current with frequency of the source, explaining the nature of its variation.
Advertisements
उत्तर
Let an alternating Emf E = E0 sinωt is applied to a series combination of inductor L, capacitor C and resistance R. Since all three of them are connected in series the current through them is same. But the voltage across each element has a different phase relation with current.
The potential difference VL, VC and VR across L, C and R at any instant is given by
VL = IXL, VC = IXC and VR = IR
Where I is the current at that instant.
XL is inductive reactance and
XC is capacitive reactance.
VR is in phase with I. VL leads I by 90° and VC lags behind I by 90°
In the phases diagram,
VL and VC are opposite to each other. If VL > VC then resultant (VL − VC) is represent by OD. OR represent the resultant of VR and (VL − VC). It is equal to the applied Emf E.
`E^2 = V_R^2 + (V_L -V_C)^2`
`E^2 =I^2 +[R^2+(X_L -X_c)^2]`
`or I =E/sqrt (R^2 + (X_2 -X_c)^2)`
The term `sqrt(R^2 +(X_2 - X_c))` is called impedance Z of the LCR circuit.
`Z = sqrt(R^2 +(X_2 -X_c)^2) =sqrt(R^2 +(L omega-1/(comega))^2)`
Emf leads current by a phase angle Φ
`tan phi = (V_L -V_C)/R = (X_L - X_c)/R =(Lomega -1/(comega))/R`
When resonance takes place
`omegaL= 1/(omegac)`
Impedance of circuit becomes equal to R. Current becomes maximum and is equal to `E/R`
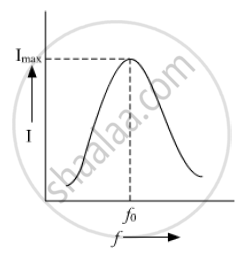
`omega_0 = 1/sqrt(LC)`
`f_0 = omega_0/(2pi) = 1/(2pisqrt(LC))`
This is the condition for resonance.
When at resonance f = f0 the current in the circuit is maximum and hence impedance of the circuit is maximum for values of f less than or greater than f0 comparatively small current flames in the circuit.
संबंधित प्रश्न
A series LCR circuit is connected across an a.c. source of variable angular frequency 'ω'. Plot a graph showing variation of current 'i' as a function of 'ω' for two resistances R1 and R2 (R1 > R2).
Answer the following questions using this graph :
(a) In which case is the resonance sharper and why?
(b) In which case in the power dissipation more and why?
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
In a series LCR circuit, obtain the condition under which watt-less current flows in the circuit ?
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
The potential difference across the resistor is 160V and that across the inductor is 120V. Find the effective value of the applied voltage. If the effective current in the circuit be 1.0 A, calculate the total impedance of the circuit.
Choose the correct answer from given options
The phase difference between the current and the voltage in series LCR circuit at resonance is
In a series LCR circuit the voltage across an inductor, capacitor and resistor are 20 V, 20 V and 40 V respectively. The phase difference between the applied voltage and the current in the circuit is ______.
Which of the following statements about a series LCR circuit connected to an ac source is correct?
To reduce the resonant frequency in an L-C-R series circuit with a generator ______.
