Advertisements
Advertisements
प्रश्न
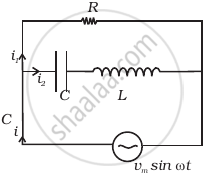
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
Advertisements
उत्तर
In the circuit given above consists of a capacitor (C) and an inductor (L) connected in series and the combination is connected in parallel with a resistance R. Due to this combination, there is an oscillation of electromagnetic energy.
Potential across R = Potential of source
P.D. across R =Vm sin ωt
i2R = Vm sin ωt
`I_2 = (V_m sin ωt)/R` ......(I)
q1 is charge on the capacitor at any time t, then for series combination of C, L applying Kirchhoff's voltage law in loop ABEFA.
VC + VL = Vm sin ωt
`q_1/C + L (di_1)/(dt)` = Vm sin ωt
`q_1/C + L (d^2q_1)/(dt^2)` = Vm sin ωt ......(II)
Let q1 = qm sin(ωt + ϕ) .......(III)
`i_1 = (dq_1)/(dt)` = qm ω cos(ωt + ϕ) .......(IV)
`(d^2q_1)/(dt^2)` = qm ω2 sin(ωt + ϕ) ......(V)
Substitute the values of equations (III) and (V) in equation (II)
`(q_m sin(ωt + ϕ))/C - Lq_m ω^2 sin(ωt + ϕ)` = Vm sin ωt
`q_m sin(ωt + ϕ) [1/C - Lω^2]` = Vm sin ωt
At ϕ = 0,
`q_m sin(ωt + ϕ) [1/C - Lω^2]` = Vm sin ωt
`q_m [1/C - Lω^2] sin ωt` = Vm sin ωt
`q_m [1/C - Lω^2]` = Vm
`q_m = V_m/(ω[1/(Cω - Lω)]` ......(VI)
Applying Kirchhoff's junction rule as junction B, i = i1 + i1 using relation I, IV
i = `(V_m sin ωt)/R + q_m ω cos(ωt + ϕ)`
Now using relation VI for qm and at ϕ = 0
i = `[(V_m sin ωt)/R + (V_m ω cos ωt)/(ω[1/(ωC) - ωL])]`
i = `V_m/R sin ωt + V_m/((1/(ωC) - ωl)) cos ωt`
Let A = `V_m/r -= C cos ϕ` ......(VII)
B = `V_m/(1/(ωC) - ωL) = C cos ϕ` ......(VIII)
i = C cos ϕ sin ωt + C sin ϕ. cos ωt
= C [cos ϕ sin ωt + sin ϕ cos ωt]
i = C sin(ωt + ϕ)
Squaring and adding (VII), (VIII)
A2 + B2 = C2 cos2ϕ + C2 sin2ϕ
= C2[cos2ϕ + sin2ϕ]
A2 + B2 = C2
or C = `sqrt(A^2 + B^2)`
ϕ = `tan^-1 B/A = tan^-1 ((V_m)/(1/(ωC) - ωL))/((V_m)/R)`
∴ `tan phi = R/((1/(ωC) - ωL))`
∵ C2 + A2 = B2 = `(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)`
C = `[(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)]^(1/2)`
∵ i = `[(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)]_2 sin(ωt + ϕ)`
I = `V_m [1/R^2 + 1/((1/(ωC) - ωL)^2)]^(1/2) sin(ωt + ϕ)` ......(IX)
And ϕ = `tan^-1 R/((1/(ωC) - ωL))`
∵ I = `V/R` or i = `V/Z`
For ac i = `V/Z sin(ωt + ϕ)` .......(X)
Comparing (IX) and (X)
So, `1/Z = [1/R^2 + 1/((1/(ωC) - ωL)^2)]^(1/2)`
This is the impedance Z for the circuit.
APPEARS IN
संबंधित प्रश्न
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
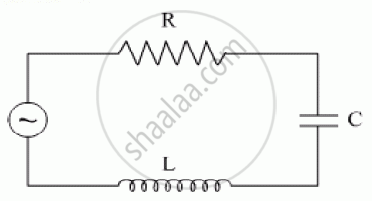
The figure shows a series LCR circuit with L = 10.0 H, C = 40 μF, R = 60 Ω connected to a variable frequency 240 V source, calculate
(i) the angular frequency of the source which drives the circuit at resonance,
(ii) the current at the resonating frequency,
(iii) the rms potential drop across the inductor at resonance.
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
The time constant of an LR circuit is 40 ms. The circuit is connected at t = 0 and the steady-state current is found to be 2.0 A. Find the current at (a) t = 10 ms (b) t = 20 ms, (c) t = 100 ms and (d) t = 1 s.
A coil having an inductance L and a resistance R is connected to a battery of emf ε. Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value to half of the steady-state value.
The magnetic field at a point inside a 2.0 mH inductor-coil becomes 0.80 of its maximum value in 20 µs when the inductor is joined to a battery. Find the resistance of the circuit.
The current in a discharging LR circuit without the battery drops from 2.0 A to 1.0 A in 0.10 s. (a) Find the time constant of the circuit. (b) If the inductance of the circuit 4.0 H, what is its resistance?
The potential difference across the resistor is 160V and that across the inductor is 120V. Find the effective value of the applied voltage. If the effective current in the circuit be 1.0 A, calculate the total impedance of the circuit.
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Derive an expression for the average power dissipated in a series LCR circuit.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
Assertion: When the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero, and so there is no current through the inductor or the capacitor.
Reason: The net current in the inductor and capacitor is zero.
A series LCR circuit contains inductance 5 mH, capacitance 2µF and resistance ion. If a frequency A.C. source is varied, what is the frequency at which maximum power is dissipated?
In series LCR circuit, the plot of Imax vs ω is shown in figure. Find the bandwidth and mark in the figure.
A series LCR circuit containing a resistance of 120 Ω has angular resonance frequency 4 × 105 rad s-1. At resonance the voltage across resistance and inductance are 60 V and 40 V respectively. At what frequency the current in the circuit lags the voltage by 45°. Give answer in ______ × 105 rad s-1.
Three students, X, Y and Z performed an experiment for studying the variation of ac with frequency in a series LCR circuit and obtained the graphs as shown below. They all used
- an AC source of the same emf and
- inductance of the same value.
- Who used minimum resistance?
- In which case will the quality Q factor be maximum?
- What did the students conclude about the nature of impedance at resonant frequency (f0)?
- An ideal capacitor is connected across 220 V, 50 Hz, and 220 V, 100 Hz supplies. Find the ratio of current flowing through it in the two cases.
To reduce the resonant frequency in an L-C-R series circuit with a generator ______.
