Question

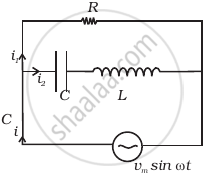
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.

Answer 1

In the circuit given above consists of a capacitor (C) and an inductor (L) connected in series and the combination is connected in parallel with a resistance R. Due to this combination, there is an oscillation of electromagnetic energy.

Potential across R = Potential of source

P.D. across R =V_m sin ωt

i₂R = V_m sin ωt

`I_2 = (V_m sin ωt)/R`  ......(I)

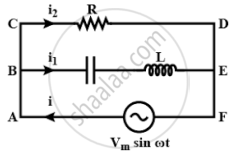
q_1​ is charge on the capacitor at any time t, then for series combination of C, L applying Kirchhoff's voltage law in loop ABEFA.

V_C + V_L = V_m sin ωt

`q_1/C + L (di_1)/(dt)` = V_m sin ωt

`q_1/C + L (d^2q_1)/(dt^2)` = V_m sin ωt  ......(II)

Let q₁ = q_m sin(ωt + ϕ)  .......(III)

`i_1 = (dq_1)/(dt)` = q_m ω cos(ωt + ϕ)  .......(IV)

`(d^2q_1)/(dt^2)` = q_m ω² sin(ωt + ϕ)  ......(V)

Substitute the values of equations (III) and (V) in equation (II)

`(q_m sin(ωt + ϕ))/C - Lq_m ω^2 sin(ωt + ϕ)` = V_m sin ωt

`q_m sin(ωt + ϕ) [1/C - Lω^2]` = V_m sin ωt

At ϕ = 0,

`q_m sin(ωt + ϕ) [1/C - Lω^2]` = V_m sin ωt

`q_m [1/C - Lω^2] sin ωt` = V_m sin ωt

`q_m [1/C - Lω^2]` = V_m

`q_m = V_m/(ω[1/(Cω - Lω)]`  ......(VI)

Applying Kirchhoff's junction rule as junction B, i = i₁ ​+ i₁​ using relation I, IV

i = `(V_m sin ωt)/R + q_m ω cos(ωt + ϕ)`

Now using relation VI for q_m and at ϕ = 0

i = `[(V_m sin ωt)/R + (V_m ω cos ωt)/(ω[1/(ωC) - ωL])]`

i = `V_m/R sin ωt + V_m/((1/(ωC) - ωl)) cos ωt`

Let A = `V_m/r -= C cos ϕ`  ......(VII)

B = `V_m/(1/(ωC) - ωL) = C cos ϕ`  ......(VIII)

i = C cos ϕ sin ωt + C sin ϕ. cos ωt

=  C [cos ϕ sin ωt + sin ϕ cos ωt]

i = C sin(ωt + ϕ)

Squaring and adding (VII), (VIII)

A² + B² = C² cos²ϕ + C² sin²ϕ

= C²[cos²ϕ + sin²ϕ]

A² + B² = C² 

or C = `sqrt(A^2 + B^2)`

ϕ = `tan^-1  B/A = tan^-1  ((V_m)/(1/(ωC) - ωL))/((V_m)/R)`

∴ `tan phi = R/((1/(ωC) - ωL))`

∵ C² + A² = B² = `(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)`

C = `[(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)]^(1/2)`

∵  i = `[(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)]_2 sin(ωt + ϕ)`

I = `V_m [1/R^2 + 1/((1/(ωC) - ωL)^2)]^(1/2) sin(ωt + ϕ)`  ......(IX)

And ϕ = `tan^-1  R/((1/(ωC) - ωL))`

∵ I = `V/R` or i = `V/Z`

For ac i = `V/Z sin(ωt + ϕ)`  .......(X)

Comparing (IX) and (X)

So, `1/Z = [1/R^2 + 1/((1/(ωC) - ωL)^2)]^(1/2)`

This is the impedance Z for the circuit.