Advertisements
Advertisements
Question
An LR circuit contains an inductor of 500 mH, a resistor of 25.0 Ω and an emf of 5.00 V in series. Find the potential difference across the resistor at t = (a) 20.0 ms, (b) 100 ms and (c) 1.00 s.
Solution
Given:-
Inductance of the inductor, L = 500 mH
Resistance of the resistor connected, R = 25 Ω
Emf of the battery, E = 5 V
For the given circuit, the potential difference across the resistance is given by
V = iR
The current in the LR circuit at time t is given by
i = i0 (1 − e−tR/L)
∴ Potential difference across the resistance at time t, V = (i0(1 − e−tR/L)R
(a) For t = 20 ms,
i = i0(1 − e−tR/L)
\[= \frac{E}{R}(1 - e^{- tR/L} )\]
\[ = \frac{5}{25}(1 - e^{- (2 \times {10}^{- 3} \times 25)/(500 \times {10}^{- 3} )} \]
\[ = \frac{1}{5}(1 - e^{- 1} ) = \frac{1}{5}(1 - 0 . 3678)\]
\[ = \frac{0 . 632}{5} = 0 . 1264 A\]
Potential difference:-
V = iR = (0.1264) × (25)
= 3.1606 V = 3.16 V
(b) For t = 100 ms,
i = i0(1 − e−tR/L)
\[= \frac{5}{25}\left( 1 - e^{( - 100 \times {10}^{- 3} ) \times (25/500 \times {10}^{- 3} )} \right)\]
\[ = \frac{1}{5}(1 - e^{- 50} )\]
\[ = \frac{1}{5}(1 - 0 . 0067)\]
\[ = \frac{0 . 9932}{5} = 0 . 19864 A\]
Potential difference:-
V = iR
= (0.19864) × (25) = 4.9665 = 4.97 V
(c) For t = 1 s,
\[i = \frac{5}{25}\left( 1 - e^{- 1 \times 25/500 \times {10}^{- 3}} \right)\]
\[ = \frac{1}{5}(1 - e^{- 50} )\]
\[ = \frac{1}{5} \times 1 = \frac{1}{5} A\]
Potential difference:-
V = iR
\[= \left( \frac{1}{5} \times 25 \right) = 5 V\]
APPEARS IN
RELATED QUESTIONS
Define 'quality factor' of resonance in a series LCR circuit. What is its SI unit?
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
A coil having an inductance L and a resistance R is connected to a battery of emf ε. Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value to half of the steady-state value.
(i) An a.c. source of emf ε = 200 sin omegat is connected to a resistor of 50 Ω . calculate :
(1) Average current (`"I"_("avg")`)
(2) Root mean square (rms) value of emf
(ii) State any two characteristics of resonance in an LCR series circuit.
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 µF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements, L, C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified for this frequency.
Obtain the resonant frequency and Q-factor of a series LCR circuit with L = 3.0 H, C = 27 µF, and R = 7.4 Ω. It is desired to improve the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way.
In series combination of R, L and C with an A.C. source at resonance, if R = 20 ohm, then impedence Z of the combination is ______.
At resonance frequency the impedance in series LCR circuit is ______.
Which of the following components of an LCR circuit, with a.c. supply, dissipates energy?
A series LCR circuit containing a 5.0 H inductor, 80 µF capacitors, and 40 Ω resistor is connected to a 230 V variable frequency ac source. The angular frequencies of the source at which power is transferred to the circuit are half the power at the resonant angular frequency are likely to be ______.
A coil of 0.01 henry inductance and 1 ohm resistance is connected to 200 volt, 50 Hz ac supply. Find the impedance of the circuit and time lag between max. alternating voltage and current.
Define Impedance.
A series LCR circuit containing a resistance of 120 Ω has angular resonance frequency 4 × 105 rad s-1. At resonance the voltage across resistance and inductance are 60 V and 40 V respectively. At what frequency the current in the circuit lags the voltage by 45°. Give answer in ______ × 105 rad s-1.
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit.
Three students, X, Y and Z performed an experiment for studying the variation of a.c. with frequency in a series LCR circuit and obtained the graphs as shown below. They all used
- an AC source of the same emf and
- inductance of the same value.
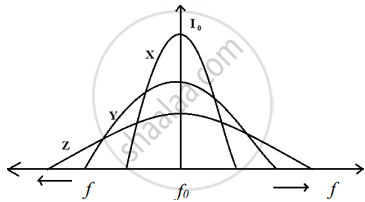
- Who used minimum resistance?
- In which case will the quality Q factor be maximum?
- What did the students conclude about the nature of impedance at resonant frequency (f0)?
- An ideal capacitor is connected across 220V, 50Hz, and 220V, 100Hz supplies. Find the ratio of current flowing through it in the two cases.
