Question

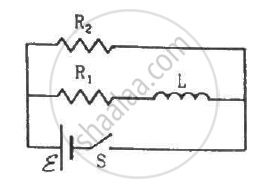
An LR circuit contains an inductor of 500 mH, a resistor of 25.0 Ω and an emf of 5.00 V in series. Find the potential difference across the resistor at t = (a) 20.0 ms, (b) 100 ms and (c) 1.00 s.

Answer 1

Given:-

Inductance of the inductor, L = 500 mH

Resistance of the resistor connected, R = 25 Ω

Emf of the battery, E = 5 V

For the given circuit, the potential difference across the resistance is given by

V = iR

The current in the LR circuit at time t is given by

i = i₀ (1 − e^−tR/L)

∴ Potential difference across the resistance at time t, V = (i₀(1 − e^−tR/L)R

(a) For t = 20 ms,

i = i₀(1 − e^−tR/L)

\[= \frac{E}{R}(1 - e^{- tR/L} )\]

\[ = \frac{5}{25}(1 - e^{- (2 \times {10}^{- 3} \times 25)/(500 \times {10}^{- 3} )} \]

\[ = \frac{1}{5}(1 - e^{- 1} ) = \frac{1}{5}(1 - 0 . 3678)\]

\[ = \frac{0 . 632}{5} = 0 . 1264 A\]

Potential difference:-

V = iR = (0.1264) × (25)

= 3.1606 V = 3.16 V

(b) For t = 100 ms,

i = i₀(1 − e^−tR/L)

\[= \frac{5}{25}\left( 1 - e^{( - 100 \times {10}^{- 3} ) \times (25/500 \times {10}^{- 3} )} \right)\]

\[ = \frac{1}{5}(1 - e^{- 50} )\]

\[ = \frac{1}{5}(1 - 0 . 0067)\]

\[ = \frac{0 . 9932}{5} = 0 . 19864 A\]

Potential difference:-

V = iR

= (0.19864) × (25) = 4.9665 = 4.97 V

(c) For t = 1 s,

\[i = \frac{5}{25}\left( 1 - e^{- 1 \times 25/500 \times {10}^{- 3}} \right)\]

\[ = \frac{1}{5}(1 - e^{- 50} )\]

\[ = \frac{1}{5} \times 1 = \frac{1}{5} A\]

Potential difference:-

V = iR

\[= \left( \frac{1}{5} \times 25 \right) = 5 V\]