Advertisements
Advertisements
Question
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
Solution
Current i in the LR circuit at time t is given by
i = i0(1 − e−t/τ)
Here,
i0 = Steady-state value of the current
(a) When the value of the current reaches 90% of the steady-state value:-
\[i = \frac{90}{100} \times i_0\]
\[\frac{90}{100} i_0\] = io(1 − e−t/τ)
⇒ 0.9 = 1 − e−t/τ
⇒ e−t/τ = 0.1
On taking natural logarithm (ln) of both sides, we get
ln (e−t/τ) = ln 0.1
`-t/tau=-2.3`
`rArr t/tau=2.3`
(b) When the value of the current reaches 99% of the steady-state value:-
\[\frac{99}{100} i_0\] = i0(1 − e−t/τ)
e−t/τ = 0.01
On taking natural logarithm (ln) of both sides, we get
ln e−t/τ = ln 0.01
`rArr -t/tau=-4.6`
`rArr t/tau=4.6`
(c) When the value of the current reaches 99.9% of the steady-state value:-
\[\frac{99 . 9}{100} i_0\] = i0(1 − e−t/τ)
⇒ e−t/τ = 0.001
On taking natural logarithm (ln) of both sides, we get
ln e−t/τ = ln 0.001
`rArr -t/tau=-6.9`
`rArr t/tau=6.9`
APPEARS IN
RELATED QUESTIONS
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
The figure shows a series LCR circuit with L = 10.0 H, C = 40 μF, R = 60 Ω connected to a variable frequency 240 V source, calculate
(i) the angular frequency of the source which drives the circuit at resonance,
(ii) the current at the resonating frequency,
(iii) the rms potential drop across the inductor at resonance.
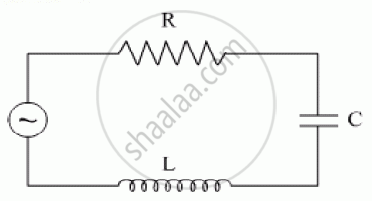
An L-R circuit has L = 1.0 H and R = 20 Ω. It is connected across an emf of 2.0 V at t = 0. Find di/dt at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1.0 s.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
What will be the potential difference in the circuit when direct current is passed through the circuit?
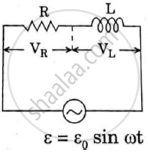
In a series, LCR circuit, obtain an expression for the resonant frequency,
Answer the following question.
What is the phase difference between the voltages across the inductor and the capacitor at resonance in the LCR circuit?
Using the phasor diagram, derive the expression for the current flowing in an ideal inductor connected to an a.c. source of voltage, v= vo sin ωt. Hence plot graphs showing the variation of (i) applied voltage and (ii) the current as a function of ωt.
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 µF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
If an LCR series circuit is connected to an ac source, then at resonance the voltage across ______.
In series combination of R, L and C with an A.C. source at resonance, if R = 20 ohm, then impedence Z of the combination is ______.
In an LCR series a.c. circuit, the voltage across each of the components, L, C and R is 50V. The voltage across the LC combination will be ______.
To reduce the resonant frequency in an LCR series circuit with a generator
The phase diffn b/w the current and voltage at resonance is
Which of the following components of an LCR circuit, with a.c. supply, dissipates energy?
Which of the following statements about a series LCR circuit connected to an ac source is correct?
An alternating voltage of 220 V is applied across a device X. A current of 0.22 A flows in the circuit and it lags behind the applied voltage in phase by π/2 radian. When the same voltage is applied across another device Y, the current in the circuit remains the same and it is in phase with the applied voltage.
- Name the devices X and Y and,
- Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
Draw a labelled graph showing variation of impedance (Z) of a series LCR circuit Vs frequency (f) of the ac supply. Mark the resonant frequency as f0·
