Advertisements
Advertisements
प्रश्न
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
उत्तर
Current i in the LR circuit at time t is given by
i = i0(1 − e−t/τ)
Here,
i0 = Steady-state value of the current
(a) When the value of the current reaches 90% of the steady-state value:-
\[i = \frac{90}{100} \times i_0\]
\[\frac{90}{100} i_0\] = io(1 − e−t/τ)
⇒ 0.9 = 1 − e−t/τ
⇒ e−t/τ = 0.1
On taking natural logarithm (ln) of both sides, we get
ln (e−t/τ) = ln 0.1
`-t/tau=-2.3`
`rArr t/tau=2.3`
(b) When the value of the current reaches 99% of the steady-state value:-
\[\frac{99}{100} i_0\] = i0(1 − e−t/τ)
e−t/τ = 0.01
On taking natural logarithm (ln) of both sides, we get
ln e−t/τ = ln 0.01
`rArr -t/tau=-4.6`
`rArr t/tau=4.6`
(c) When the value of the current reaches 99.9% of the steady-state value:-
\[\frac{99 . 9}{100} i_0\] = i0(1 − e−t/τ)
⇒ e−t/τ = 0.001
On taking natural logarithm (ln) of both sides, we get
ln e−t/τ = ln 0.001
`rArr -t/tau=-6.9`
`rArr t/tau=6.9`
APPEARS IN
संबंधित प्रश्न
Why does current in a steady state not flow in a capacitor connected across a battery? However momentary current does flow during charging or discharging of the capacitor. Explain.
Show that in an a.c. circuit containing a pure inductor, the voltage is ahead of current by π/2 in phase ?
An LR circuit having a time constant of 50 ms is connected with an ideal battery of emf ε. find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and (c) the magnetic field energy stored in the circuit reaches half its maximum value.
A coil having an inductance L and a resistance R is connected to a battery of emf ε. Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value to half of the steady-state value.
An inductor of inductance 2.00 H is joined in series with a resistor of resistance 200 Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) the current in the circuit, (b) the power delivered by the battery, (c) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Answer the following question.
What is the phase difference between the voltages across the inductor and the capacitor at resonance in the LCR circuit?
Obtain the resonant frequency and Q-factor of a series LCR circuit with L = 3.0 H, C = 27 µF, and R = 7.4 Ω. It is desired to improve the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way.
If an LCR series circuit is connected to an ac source, then at resonance the voltage across ______.
Assertion: When the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero, and so there is no current through the inductor or the capacitor.
Reason: The net current in the inductor and capacitor is zero.
At resonance frequency the impedance in series LCR circuit is ______.
A series LCR circuit containing a 5.0 H inductor, 80 µF capacitors, and 40 Ω resistor is connected to a 230 V variable frequency ac source. The angular frequencies of the source at which power is transferred to the circuit are half the power at the resonant angular frequency are likely to be ______.
A series LCR circuit containing 5.0 H inductor, 80 µF capacitor and 40 Ω resistor is connected to 230 V variable frequency ac source. The angular frequencies of the source at which power transferred to the circuit is half the power at the resonant angular frequency are likely to be ______.
To reduce the resonant frequency in an LCR series circuit with a generator ______.
A coil of 0.01 henry inductance and 1 ohm resistance is connected to 200 volt, 50 Hz ac supply. Find the impedance of the circuit and time lag between max. alternating voltage and current.
A series LCR circuit driven by 300 V at a frequency of 50 Hz contains a resistance R = 3 kΩ, an inductor of inductive reactance XL = 250 πΩ, and an unknown capacitor. The value of capacitance to maximize the average power should be ______.
Draw the impedance triangle for a series LCR AC circuit and write the expressions for the impedance and the phase difference between the emf and the current.
Three students, X, Y and Z performed an experiment for studying the variation of a.c. with frequency in a series LCR circuit and obtained the graphs as shown below. They all used
- an AC source of the same emf and
- inductance of the same value.
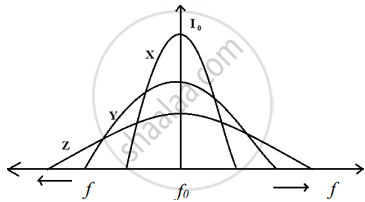
- Who used minimum resistance?
- In which case will the quality Q factor be maximum?
- What did the students conclude about the nature of impedance at resonant frequency (f0)?
- An ideal capacitor is connected across 220V, 50Hz, and 220V, 100Hz supplies. Find the ratio of current flowing through it in the two cases.
