Advertisements
Advertisements
Question
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
Advertisements
Solution
Inductance, L = 0.12 H
Capacitance, C = 480 nF = 480 × 10−9 F
Resistance, R = 23 Ω
Supply voltage, V = 230 V
Peak voltage is given as:
V0 = `sqrt2 xx 230` = 325.22 V
(a) Current flowing in the circuit is given by the relation,
I0 = `"V"_0/(sqrt("R"^2 + (ω"L" - 1/(ω"C"))^2`
Where,
I0 = maximum at resonance
At resonance, we have
`ω_"R""L" - 1/(ω_"R""C")` = 0
Where,
ωR = Resonance angular frequency
∴ ωR = `1/sqrt("LC")`
= `1/sqrt(0.12 xx 480 xx 10^-9)`
= 4166.67 rad/s
∴ Resonant frequency, vR = `ω_"R"/(2π) = 4166.67/(2 xx 3.14)` = 663.48 Hz
And, maximum current `("I"_0)_"Max" = "V"_0/"R" = 325.22/23` = 14.14 A
(b) Maximum average power absorbed by the circuit is given as:
`("P"_"av")_"Max" = 1/2 ("I"_0)_"Max"^2 "R"`
= `1/2 xx (14.14)^2 xx 23`
= 2299.3 W
Hence, resonant frequency (vR) is 663.48 Hz.
(c) The power transferred to the circuit is half the power at resonant frequency.
Frequencies at which power transferred is half, = ωR ± Δω
= `2π ("v"_"R" ± Δ"v")`
Where,
Δω = `"R"/(2"L")`
= `23/(2 xx 0.12)`
= 95.83 rad/s
Hence, change in frequency, Δv = `1/(2π)Δω = 95.83/(2π)` = 15.26 Hz
∴ vR + Δv = 663.48 + 15.26 = 678.74 Hz
And, vR − Δv = 663.48 − 15.26 = 648.22 Hz
Hence, at 648.22 Hz and 678.74 Hz frequencies, the power transferred is half.
At these frequencies, current amplitude can be given as:
I' = `1/sqrt2 xx ("I"_0)_"Max"`
= `14.14/sqrt2`
= 10 A
(d) Q-factor of the given circuit can be obtained using the relation, Q = `(ω_"R""L")/"R"`
= `(4166.67 xx 0.12)/23`
= 21.74
Hence, the Q-factor of the given circuit is 21.74.
APPEARS IN
RELATED QUESTIONS
In a series LCR circuit, obtain the condition under which watt-less current flows in the circuit ?
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit. Plot a graph to show the variation of current with frequency of the source, explaining the nature of its variation.
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
Two coils A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10 Ω. Each coil is connected to an ideal battery of emf 2.0 V at t = 0. Let iA and iBbe the currents in the two circuit at time t. Find the ratio iA / iB at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1 s.
Use the expression for Lorentz force acting on the charge carriers of a conductor to obtain the expression for the induced emf across the conductor of length l moving with velocity v through a magnetic field B acting perpendicular to its length.
Derive an expression for the average power dissipated in a series LCR circuit.
The selectivity of a series LCR a.c. circuit is large, when ______.
Choose the correct answer from given options
The phase difference between the current and the voltage in series LCR circuit at resonance is
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 µF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
In an L.C.R. series a.c. circuit, the current ______.
At resonance frequency the impedance in series LCR circuit is ______.
The resonant frequency of a RF oscillator is 1 MHz and its bandwidth is 10 kHz. The quality factor will be :
To reduce the resonant frequency in an LCR series circuit with a generator
In series LCR circuit, the plot of Imax vs ω is shown in figure. Find the bandwidth and mark in the figure.
A series LCR circuit driven by 300 V at a frequency of 50 Hz contains a resistance R = 3 kΩ, an inductor of inductive reactance XL = 250 πΩ, and an unknown capacitor. The value of capacitance to maximize the average power should be ______.
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit.
Three students, X, Y and Z performed an experiment for studying the variation of ac with frequency in a series LCR circuit and obtained the graphs as shown below. They all used
- an AC source of the same emf and
- inductance of the same value.
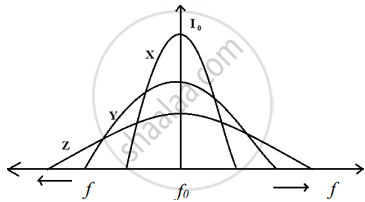
- Who used minimum resistance?
- In which case will the quality Q factor be maximum?
- What did the students conclude about the nature of impedance at resonant frequency (f0)?
- An ideal capacitor is connected across 220 V, 50 Hz, and 220 V, 100 Hz supplies. Find the ratio of current flowing through it in the two cases.
In the given circuit, rms value of current (Irms) through the resistor R is:
