Advertisements
Advertisements
प्रश्न
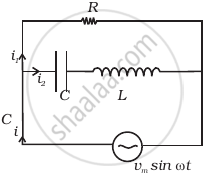
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
Advertisements
उत्तर
In the circuit given above consists of a capacitor (C) and an inductor (L) connected in series and the combination is connected in parallel with a resistance R. Due to this combination, there is an oscillation of electromagnetic energy.
Potential across R = Potential of source
P.D. across R =Vm sin ωt
i2R = Vm sin ωt
`I_2 = (V_m sin ωt)/R` ......(I)
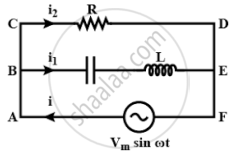
q1 is charge on the capacitor at any time t, then for series combination of C, L applying Kirchhoff's voltage law in loop ABEFA.
VC + VL = Vm sin ωt
`q_1/C + L (di_1)/(dt)` = Vm sin ωt
`q_1/C + L (d^2q_1)/(dt^2)` = Vm sin ωt ......(II)
Let q1 = qm sin(ωt + ϕ) .......(III)
`i_1 = (dq_1)/(dt)` = qm ω cos(ωt + ϕ) .......(IV)
`(d^2q_1)/(dt^2)` = qm ω2 sin(ωt + ϕ) ......(V)
Substitute the values of equations (III) and (V) in equation (II)
`(q_m sin(ωt + ϕ))/C - Lq_m ω^2 sin(ωt + ϕ)` = Vm sin ωt
`q_m sin(ωt + ϕ) [1/C - Lω^2]` = Vm sin ωt
At ϕ = 0,
`q_m sin(ωt + ϕ) [1/C - Lω^2]` = Vm sin ωt
`q_m [1/C - Lω^2] sin ωt` = Vm sin ωt
`q_m [1/C - Lω^2]` = Vm
`q_m = V_m/(ω[1/(Cω - Lω)]` ......(VI)
Applying Kirchhoff's junction rule as junction B, i = i1 + i1 using relation I, IV
i = `(V_m sin ωt)/R + q_m ω cos(ωt + ϕ)`
Now using relation VI for qm and at ϕ = 0
i = `[(V_m sin ωt)/R + (V_m ω cos ωt)/(ω[1/(ωC) - ωL])]`
i = `V_m/R sin ωt + V_m/((1/(ωC) - ωl)) cos ωt`
Let A = `V_m/r -= C cos ϕ` ......(VII)
B = `V_m/(1/(ωC) - ωL) = C cos ϕ` ......(VIII)
i = C cos ϕ sin ωt + C sin ϕ. cos ωt
= C [cos ϕ sin ωt + sin ϕ cos ωt]
i = C sin(ωt + ϕ)
Squaring and adding (VII), (VIII)
A2 + B2 = C2 cos2ϕ + C2 sin2ϕ
= C2[cos2ϕ + sin2ϕ]
A2 + B2 = C2
or C = `sqrt(A^2 + B^2)`
ϕ = `tan^-1 B/A = tan^-1 ((V_m)/(1/(ωC) - ωL))/((V_m)/R)`
∴ `tan phi = R/((1/(ωC) - ωL))`
∵ C2 + A2 = B2 = `(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)`
C = `[(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)]^(1/2)`
∵ i = `[(V_m^2)/R^2 + (V_m^2)/((1/(ωC) - ωL)^2)]_2 sin(ωt + ϕ)`
I = `V_m [1/R^2 + 1/((1/(ωC) - ωL)^2)]^(1/2) sin(ωt + ϕ)` ......(IX)
And ϕ = `tan^-1 R/((1/(ωC) - ωL))`
∵ I = `V/R` or i = `V/Z`
For ac i = `V/Z sin(ωt + ϕ)` .......(X)
Comparing (IX) and (X)
So, `1/Z = [1/R^2 + 1/((1/(ωC) - ωL)^2)]^(1/2)`
This is the impedance Z for the circuit.
APPEARS IN
संबंधित प्रश्न
In a series LCR circuit connected to an a.c. source of voltage v = vmsinωt, use phasor diagram to derive an expression for the current in the circuit. Hence, obtain the expression for the power dissipated in the circuit. Show that power dissipated at resonance is maximum
A series LCR circuit is connected across an a.c. source of variable angular frequency 'ω'. Plot a graph showing variation of current 'i' as a function of 'ω' for two resistances R1 and R2 (R1 > R2).
Answer the following questions using this graph :
(a) In which case is the resonance sharper and why?
(b) In which case in the power dissipation more and why?
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
The figure shows a series LCR circuit with L = 10.0 H, C = 40 μF, R = 60 Ω connected to a variable frequency 240 V source, calculate
(i) the angular frequency of the source which drives the circuit at resonance,
(ii) the current at the resonating frequency,
(iii) the rms potential drop across the inductor at resonance.
Derive an expression for the average power consumed in a series LCR circuit connected to a.c. source in which the phase difference between the voltage and the current in the circuit is Φ.
An inductor of inductance 2.00 H is joined in series with a resistor of resistance 200 Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) the current in the circuit, (b) the power delivered by the battery, (c) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
The potential difference across the resistor is 160V and that across the inductor is 120V. Find the effective value of the applied voltage. If the effective current in the circuit be 1.0 A, calculate the total impedance of the circuit.
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Derive an expression for the average power dissipated in a series LCR circuit.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements, L, C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified for this frequency.
If an LCR series circuit is connected to an ac source, then at resonance the voltage across ______.
A coil of 40 henry inductance is connected in series with a resistance of 8 ohm and the combination is joined to the terminals of a 2 volt battery. The time constant of the circuit is ______.
In a series LCR circuit the voltage across an inductor, capacitor and resistor are 20 V, 20 V and 40 V respectively. The phase difference between the applied voltage and the current in the circuit is ______.
At resonant frequency the current amplitude in series LCR circuit is ______.
A series LCR circuit containing a resistance of 120 Ω has angular resonance frequency 4 × 105 rad s-1. At resonance the voltage across resistance and inductance are 60 V and 40 V respectively. At what frequency the current in the circuit lags the voltage by 45°. Give answer in ______ × 105 rad s-1.
Draw the phasor diagram for a series LRC circuit connected to an AC source.
Draw a labelled graph showing variation of impedance (Z) of a series LCR circuit Vs frequency (f) of the ac supply. Mark the resonant frequency as f0·
A series LCR circuit (L = 10 H, C = 10 µF, R = 50 Ω) is connected to V = 200 sin (100t). If ν0 is the resonant frequency and ν is the source frequency, then ______.
Which of the following combinations should be selected for better tuning of an L-C-R circuit used for communication?
