Advertisements
Advertisements
प्रश्न
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
Advertisements
उत्तर
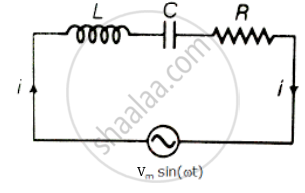
Consider L-C-R series circuit with AC supply
V = Vm sin ωt
Applying voltage Kirchhoff's law over the circuit
∴ VL + VC + VR = Vm sin ωt
L = `(di)/(dt) + Ri + q/c` = Vi = Vm sin ωt
Multiply the above equation by i on both the sides.
L = `(di)/(dt) + Ri + q/c` = Vi = Vm sin ωt
Multiply the above equation by `1/2` on both sides
`1/2 Li (di)/(dt) + i q/(2C) + (i^2R)/2 = 1/2` Vmi sin ωt `(∵ i = (dq)/(dt))`
`(d(1/2 Li^2))/(dt) + 1/(2C) (dq^2)/(dt) + (i^2R)/2 = 1/2` Vmi sin ωt .....(I)
(i) `(d(1/2 li^2))/(dt)` Represents the rate of change of potential energy in inductance L.
(ii) `d/(dt) q^2/(2C)` represents energy stored in dt time in the capacitor.
(iii) i2R represents joules heating loss.
(iv) `1/2 V_m i` sin ωt is the rate at which driving force pours in energy. It goes into ohmic loss and increase of stored energy in capacitor and inductor.
Vi = rate at which driving force pours in energy. It goes into (i) ohmic loss and (ii) increase of stored energy.
Hence equation (ii) is in the form of conservation of energy statement. Integrating both sides of equation. (ii) with respect to time over one full cycle (0 → T) we may write
`int_0^T d/(dt) (1/2 Li^2 + q^2/(2C)) dt + int_0^T Ri^2 dt = int_0^T Vi dt`
⇒ 0 + (+ ve) = `int_0^T Vi dt`
⇒ `int_0^T Vi dt > 0` if phase difference between V and i is a constant and acute angle.
APPEARS IN
संबंधित प्रश्न
Define 'quality factor' of resonance in a series LCR circuit. What is its SI unit?
A series LCR circuit is connected across an a.c. source of variable angular frequency 'ω'. Plot a graph showing variation of current 'i' as a function of 'ω' for two resistances R1 and R2 (R1 > R2).
Answer the following questions using this graph :
(a) In which case is the resonance sharper and why?
(b) In which case in the power dissipation more and why?
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
Derive an expression for the average power consumed in a series LCR circuit connected to a.c. source in which the phase difference between the voltage and the current in the circuit is Φ.
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
A coil of resistance 40 Ω is connected across a 4.0 V battery. 0.10 s after the battery is connected, the current in the coil is 63 mA. Find the inductance of the coil.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
A coil having an inductance L and a resistance R is connected to a battery of emf ε. Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value to half of the steady-state value.
(i) An a.c. source of emf ε = 200 sin omegat is connected to a resistor of 50 Ω . calculate :
(1) Average current (`"I"_("avg")`)
(2) Root mean square (rms) value of emf
(ii) State any two characteristics of resonance in an LCR series circuit.
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Derive an expression for the average power dissipated in a series LCR circuit.
The selectivity of a series LCR a.c. circuit is large, when ______.
In an L.C.R. series a.c. circuit, the current ______.
In an LCR circuit having L = 8 henery. C = 0.5 µF and R = 100 ohm in series, the resonance frequency in radian/sec is
A series LCR circuit containing a 5.0 H inductor, 80 µF capacitors, and 40 Ω resistor is connected to a 230 V variable frequency ac source. The angular frequencies of the source at which power is transferred to the circuit are half the power at the resonant angular frequency are likely to be ______.
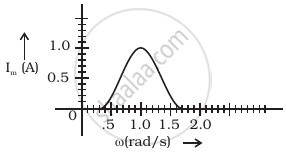
In series LCR circuit, the plot of Imax vs ω is shown in figure. Find the bandwidth and mark in the figure.
A coil of 0.01 henry inductance and 1 ohm resistance is connected to 200 volt, 50 Hz ac supply. Find the impedance of the circuit and time lag between max. alternating voltage and current.
An alternating voltage of 220 V is applied across a device X. A current of 0.22 A flows in the circuit and it lags behind the applied voltage in phase by π/2 radian. When the same voltage is applied across another device Y, the current in the circuit remains the same and it is in phase with the applied voltage.
- Name the devices X and Y and,
- Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
Draw the impedance triangle for a series LCR AC circuit and write the expressions for the impedance and the phase difference between the emf and the current.
