Advertisements
Advertisements
प्रश्न
Derive an expression for the average power dissipated in a series LCR circuit.
उत्तर
We have seen that a voltage v = vm sin ωt applied to a series RLC circuit drives a current in the circuit given by `"i" = "i"_"m" sin(omega t + ∅)` Where
`"I"_"m" = "v"_"m"/"z" and ∅ = tan^-1 (("X"_"c"-"X"_"L")/("R"))`
Therefore, the instantaneous power p supplied by the source is
`"p" = "vi" = ("v"_"m"sin omega t) xx ["i"_"m" sin(omega t + ∅)]`
= `("v"_"m""i"_"m")/(2)[cos ∅ - cos(2omega t + ∅)]`
The average power over a cycle is given by the average of the two terms in R.H.S. of the above equation. It is only the second term which is time-dependent. Its average is zero (the positive half of the cosine cancels the negative half). Therefore,
`"P" = ("v"_"m""i"_"m")/(2) cos ∅ = ("v"_"m")/sqrt2 ("i"_"m")/sqrt2 cos ∅`
= `"V" "I" cos ∅`
This can also be written as
`"P" = "I"^2 "Z"cos ∅`
So, the average power dissipated depends not only on the voltage and current but also on the cosine of the phase angle ∅ between them. The quantity cos ∅ is called the power factor.
APPEARS IN
संबंधित प्रश्न
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
Why does current in a steady state not flow in a capacitor connected across a battery? However momentary current does flow during charging or discharging of the capacitor. Explain.
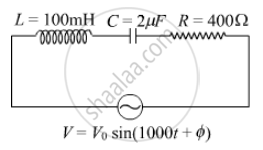
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?
(ii) Without making any other change, find the value of the additional capacitor C1, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
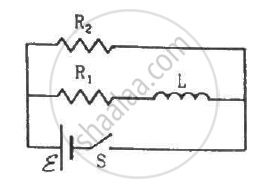
Consider the circuit shown in figure. (a) Find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c) Find the current through the inductor after one time constant.
In a series, LCR circuit, obtain an expression for the resonant frequency,
Choose the correct answer from given options
The selectivity of a series LCR a.c. circuit is large, when
Choose the correct answer from given options
The phase difference between the current and the voltage in series LCR circuit at resonance is
A series LCR circuit contains inductance 5 mH, capacitance 2µF and resistance ion. If a frequency A.C. source is varied, what is the frequency at which maximum power is dissipated?
In series LCR AC-circuit, the phase angle between current and voltage is
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
