Advertisements
Advertisements
प्रश्न
State Gauss's law in electrostatics. Show, with the help of a suitable example along with the figure, that the outward flux due to a point charge 'q'. in vacuum within a closed surface, is independent of its size or shape and is given by `q/ε_0`
उत्तर
Statement: The electric flux linked with a closed surface is equal to `(1)/ε_0` times the net charge enclosed by a closed surface.
Mathematical expression :
`Ø_"E" = oint vec"E".dvec"s" = (1)/(ε_0) (q_"net")`
Consider two spherical surfaces of radius r and 2r respectively and a charge 1 is enclosed in it. According to gauss theorem, the total electric flux linked with a closed surface depends on the charge enclosed in it so
(a)
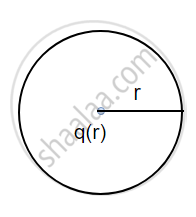
(b)
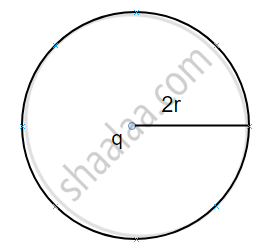
`Ø_E = q/ε_0 "and for fig"("b")`
`Ø_E = q/ε_0`.
APPEARS IN
संबंधित प्रश्न
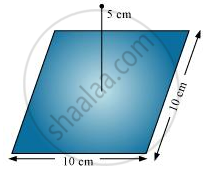
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
Gaussian surface cannot pass through discrete charge because ____________.
q1, q2, q3 and q4 are point charges located at points as shown in the figure and S is a spherical gaussian surface of radius R. Which of the following is true according to the Gauss' law?

Gauss' law helps in ______
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then
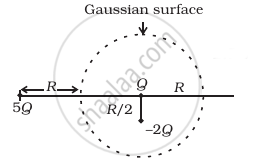
- total flux through the surface of the sphere is `(-Q)/ε_0`.
- field on the surface of the sphere is `(-Q)/(4 piε_0 R^2)`.
- flux through the surface of sphere due to 5Q is zero.
- field on the surface of sphere due to –2Q is same everywhere.
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
