Advertisements
Advertisements
प्रश्न
Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then
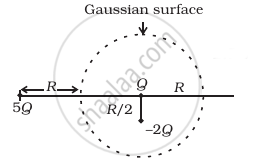
- total flux through the surface of the sphere is `(-Q)/ε_0`.
- field on the surface of the sphere is `(-Q)/(4 piε_0 R^2)`.
- flux through the surface of sphere due to 5Q is zero.
- field on the surface of sphere due to –2Q is same everywhere.
विकल्प
a and d
a and c
b and d
c and d
उत्तर
a and c
Explanation:
From Gauss' law, we know `oint_s vecE * dvecS = q_(enclosed)/ε_0`.
Thus, from figure, Total charge inside the Gaussian surface `q_(enclosed)` = Q – 2Q = – Q
The charge 5Q lies outside the surface, thus it makes no contribution to electric flux through the given surface.
APPEARS IN
संबंधित प्रश्न
A thin conducting spherical shell of radius R has charge Q spread uniformly over its surface. Using Gauss’s law, derive an expression for an electric field at a point outside the shell.
Gaussian surface cannot pass through discrete charge because ____________.
The Gaussian surface ______.
The surface considered for Gauss’s law is called ______.
The Electric flux through the surface
 (i) |
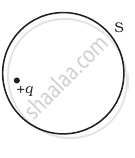 (ii) |
 (iii) |
 (iv) |
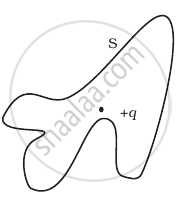
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
If there were only one type of charge in the universe, then ______.
- `oint_s` E.dS ≠ 0 on any surface.
- `oint_s` E.dS = 0 if the charge is outside the surface.
- `oint_s` E.dS could not be defined.
- `oint_s` E.dS = `q/ε_0` if charges of magnitude q were inside the surface.
Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region
- the electric field is necessarily zero.
- the electric field is due to the dipole moment of the charge distribution only.
- the dominant electric field is `∞ 1/r^3`, for large r, where r is the distance from a origin in this region.
- the work done to move a charged particle along a closed path, away from the region, will be zero.
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
