Advertisements
Advertisements
प्रश्न
Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then
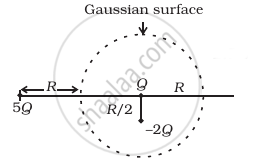
- total flux through the surface of the sphere is `(-Q)/ε_0`.
- field on the surface of the sphere is `(-Q)/(4 piε_0 R^2)`.
- flux through the surface of sphere due to 5Q is zero.
- field on the surface of sphere due to –2Q is same everywhere.
पर्याय
a and d
a and c
b and d
c and d
उत्तर
a and c
Explanation:
From Gauss' law, we know `oint_s vecE * dvecS = q_(enclosed)/ε_0`.
Thus, from figure, Total charge inside the Gaussian surface `q_(enclosed)` = Q – 2Q = – Q
The charge 5Q lies outside the surface, thus it makes no contribution to electric flux through the given surface.
APPEARS IN
संबंधित प्रश्न
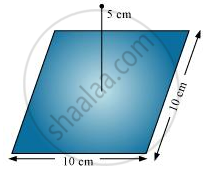
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
State Gauss’s law for magnetism. Explain its significance.
Answer the following question.
State Gauss's law on electrostatics and drive expression for the electric field due to a long straight thin uniformly charged wire (linear charge density λ) at a point lying at a distance r from the wire.
The Gaussian surface ______.
Which of the following statements is not true about Gauss’s law?
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
The region between two concentric spheres of radii a < b contain volume charge density ρ(r) = `"c"/"r"`, where c is constant and r is radial- distanct from centre no figure needed. A point charge q is placed at the origin, r = 0. Value of c is in such a way for which the electric field in the region between the spheres is constant (i.e. independent of r). Find the value of c:
In finding the electric field using Gauss law the formula `|vec"E"| = "q"_"enc"/(epsilon_0|"A"|)` is applicable. In the formula ε0 is permittivity of free space, A is the area of Gaussian surface and qenc is charge enclosed by the Gaussian surface. This equation can be used in which of the following situation?
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
