Advertisements
Advertisements
प्रश्न
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
उत्तर
a. Let the Universe have a radius of R. Assume that the hydrogen atoms are uniformly distributed. The charge on each hydrogen atom is
`e_H = – (1 + y) e + e = – ye = |ye|`
The mass of each hydrogen atom is ~ mp (mass of proton). Expansion starts if the Coulumb repulsion on a hydrogen atom, at R, is larger than the gravitational attraction. Let the Electric Field at R be E. Then
`4piR^2 E = 4/(3ε_0) pi R^3 N |ye|` ....(Gauss's law)
E(R) = `1/3 (N|ye|)/ε_0 R hatr`
Let the gravitational field at R be GR. Then
`- 4piR^2 G_R = 4 piG m_p 4/3 piR^3 N`
`G_R = - 4/3 pi Gm_pN R`
`G_R (R) = - 4/3 pi Gm_pN R hatr`
Thus the Coulombic force on a hydrogen atom at R is
yeE(R) = `1/3 (Ny^2e^2)/ε_0 R hatr`
The gravitional force on this atom is
mpGr (R) = `- (4pi)/3 GNm_p^2 R hatr`
The net force on the atom is
F = `(1/3 (Ny^2e^2)/ε_0 R - (4pi)/3 GNm_p^2R)hatr`
The critical value is when
`1/3 (Ny^2e^2)/ε_0 R = (4pi)/3 GNm_p^2R`
⇒ `y_c^2 = 4piε_0 G m_p^2/e^2`
= `(7 xx 10^-11 xx 1.8^2 xx 10^6 xx 81 xx 10^-62)/(9 xx 10^9 xx 1.6^2 xx 10^-38)`
= 63 × 10–38
∴ yc = 8 × 10–19 = 10–18
b. Because of the net force, the hydrogen atom experiences an acceleration such that
`m_p (d^2R)/(dt^2) = (1/3 (Ny^2e^2)/e_o R - (4p)/3 GNm_p^2 R)`
Or, `(d^2R)/(dt^2) = a^2R` where `alpha^2 = 1/m_p (1/3 (Ny^2e^2)/e_o - (4p)/3 GNm_p^2)`
This has a solution R = `Ae^(at) + Be^(-at)`
As we are seeking an expansion, B = 0.
∴ R = Aeat
⇒ R = αAeat = αR
Thus, the velocity is proportional to the distance from the centre.
APPEARS IN
संबंधित प्रश्न
State and explain Gauss’s law.
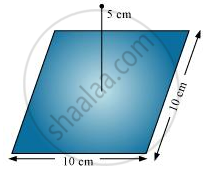
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
A thin conducting spherical shell of radius R has charge Q spread uniformly over its surface. Using Gauss’s law, derive an expression for an electric field at a point outside the shell.
Answer the following question.
State Gauss's law for magnetism. Explain its significance.
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
The region between two concentric spheres of radii a < b contain volume charge density ρ(r) = `"c"/"r"`, where c is constant and r is radial- distanct from centre no figure needed. A point charge q is placed at the origin, r = 0. Value of c is in such a way for which the electric field in the region between the spheres is constant (i.e. independent of r). Find the value of c:
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
