Advertisements
Advertisements
प्रश्न
Answer the following question.
State Gauss's law for magnetism. Explain its significance.
उत्तर
The net magnetic flux (ΦB) through any closed surface is always zero.
This law suggests that the number of magnetic field lines leaving any closed surface is always equal to the number of magnetic field lines entering it.

Suppose a closed surface S is held in a uniform magnetic field `vecB`.
Consider a small vector area element Δ`vec"S"` of this surface.
Magnetic flux through this area element is defined as ΔΦB = `vec"B".Δvec"S" `
Considering all small area elements of the surface, we obtain net magnetic flux through the surface as:
ØB = `sum_"All" ΔØ_"B" = sum_"All" vec"B". Δvec"S" = 0`
APPEARS IN
संबंधित प्रश्न
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
Gaussian surface cannot pass through discrete charge because ____________.
q1, q2, q3 and q4 are point charges located at points as shown in the figure and S is a spherical gaussian surface of radius R. Which of the following is true according to the Gauss' law?

The Gaussian surface ______.
Gauss' law helps in ______
The Electric flux through the surface
 (i) |
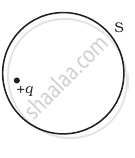 (ii) |
 (iii) |
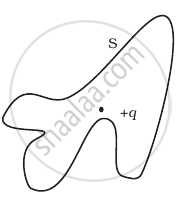 (iv) |
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
