Advertisements
Advertisements
प्रश्न
The Electric flux through the surface
 (i) |
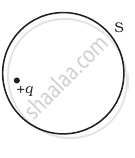 (ii) |
 (iii) |
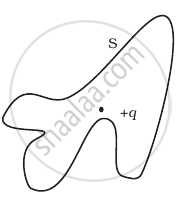 (iv) |
पर्याय
in Figure (iv) is the largest.
in Figure (iii) is the least.
in Figure (ii) is same as Figure (iii) but is smaller than Figure (iv)
is the same for all the figures.
उत्तर
is the same for all the figures.
Explanation:
According to Gauss’ law of electrostatics, the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity,
i.e., `phi = (Q_(enclosed))/ε_0`
Thus, electric flux through a surface doesn’t depend on the shape, size or area of a surface but it depends on the amount of charge enclosed by the surface.
In the given figures the charge enclosed is the same that means the electric flux through all the surfaces should be the same.
APPEARS IN
संबंधित प्रश्न
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
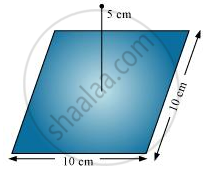
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0 ≤ r ≤ ∞.
The Gaussian surface ______.
The surface considered for Gauss’s law is called ______.
Which of the following statements is not true about Gauss’s law?
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then
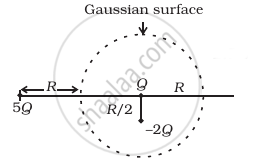
- total flux through the surface of the sphere is `(-Q)/ε_0`.
- field on the surface of the sphere is `(-Q)/(4 piε_0 R^2)`.
- flux through the surface of sphere due to 5Q is zero.
- field on the surface of sphere due to –2Q is same everywhere.
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
