Advertisements
Advertisements
Question
The Electric flux through the surface
 (i) |
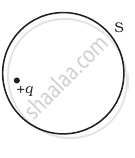 (ii) |
 (iii) |
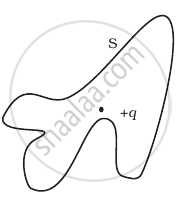 (iv) |
Options
in Figure (iv) is the largest.
in Figure (iii) is the least.
in Figure (ii) is same as Figure (iii) but is smaller than Figure (iv)
is the same for all the figures.
Solution
is the same for all the figures.
Explanation:
According to Gauss’ law of electrostatics, the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity,
i.e., `phi = (Q_(enclosed))/ε_0`
Thus, electric flux through a surface doesn’t depend on the shape, size or area of a surface but it depends on the amount of charge enclosed by the surface.
In the given figures the charge enclosed is the same that means the electric flux through all the surfaces should be the same.
APPEARS IN
RELATED QUESTIONS
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0 ≤ r ≤ ∞.
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
Answer the following question.
State Gauss's law on electrostatics and drive expression for the electric field due to a long straight thin uniformly charged wire (linear charge density λ) at a point lying at a distance r from the wire.
The surface considered for Gauss’s law is called ______.
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
If there were only one type of charge in the universe, then ______.
- `oint_s` E.dS ≠ 0 on any surface.
- `oint_s` E.dS = 0 if the charge is outside the surface.
- `oint_s` E.dS could not be defined.
- `oint_s` E.dS = `q/ε_0` if charges of magnitude q were inside the surface.
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
In finding the electric field using Gauss law the formula `|vec"E"| = "q"_"enc"/(epsilon_0|"A"|)` is applicable. In the formula ε0 is permittivity of free space, A is the area of Gaussian surface and qenc is charge enclosed by the Gaussian surface. This equation can be used in which of the following situation?
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
