Advertisements
Advertisements
Question
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
Options
`Q/epsi_0`
`Q/(6epsi_0)`
`Q/(8epsi_0)`
`Q/(3epsi_0)`
Solution
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is `underlinebb(Q/(6epsi_0))`.
Explanation:
Assuming the cube as a Gaussian surface, the total flux passing through the cube of side l can be given as,
`phi = Q/epsi_0`
Flux through each face of the cube: As the charge is placed symmetrically to each face of the cube, thus electric flux passing through each face is equal.
∴ Electric flux passing through each face,
`phi^' = phi/6 = Q/(6epsi_0)`
APPEARS IN
RELATED QUESTIONS
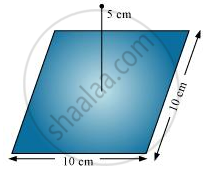
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
A thin conducting spherical shell of radius R has charge Q spread uniformly over its surface. Using Gauss’s law, derive an expression for an electric field at a point outside the shell.
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0 ≤ r ≤ ∞.
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
State Gauss's law in electrostatics. Show, with the help of a suitable example along with the figure, that the outward flux due to a point charge 'q'. in vacuum within a closed surface, is independent of its size or shape and is given by `q/ε_0`
Gaussian surface cannot pass through discrete charge because ____________.
Gauss' law helps in ______
The Electric flux through the surface
 (i) |
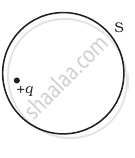 (ii) |
 (iii) |
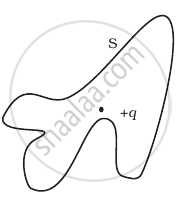 (iv) |
If there were only one type of charge in the universe, then ______.
- `oint_s` E.dS ≠ 0 on any surface.
- `oint_s` E.dS = 0 if the charge is outside the surface.
- `oint_s` E.dS could not be defined.
- `oint_s` E.dS = `q/ε_0` if charges of magnitude q were inside the surface.
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
