Advertisements
Advertisements
Question
State Gauss's law in electrostatics. Show, with the help of a suitable example along with the figure, that the outward flux due to a point charge 'q'. in vacuum within a closed surface, is independent of its size or shape and is given by `q/ε_0`
Solution
Statement: The electric flux linked with a closed surface is equal to `(1)/ε_0` times the net charge enclosed by a closed surface.
Mathematical expression :
`Ø_"E" = oint vec"E".dvec"s" = (1)/(ε_0) (q_"net")`
Consider two spherical surfaces of radius r and 2r respectively and a charge 1 is enclosed in it. According to gauss theorem, the total electric flux linked with a closed surface depends on the charge enclosed in it so
(a)
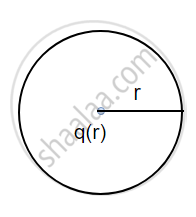
(b)
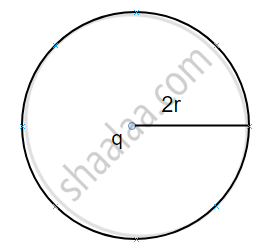
`Ø_E = q/ε_0 "and for fig"("b")`
`Ø_E = q/ε_0`.
APPEARS IN
RELATED QUESTIONS
State and explain Gauss’s law.
Answer the following question.
State Gauss's law on electrostatics and drive expression for the electric field due to a long straight thin uniformly charged wire (linear charge density λ) at a point lying at a distance r from the wire.
The surface considered for Gauss’s law is called ______.
Which of the following statements is not true about Gauss’s law?
If `oint_s` E.dS = 0 over a surface, then ______.
- the electric field inside the surface and on it is zero.
- the electric field inside the surface is necessarily uniform.
- the number of flux lines entering the surface must be equal to the number of flux lines leaving it.
- all charges must necessarily be outside the surface.
If there were only one type of charge in the universe, then ______.
- `oint_s` E.dS ≠ 0 on any surface.
- `oint_s` E.dS = 0 if the charge is outside the surface.
- `oint_s` E.dS could not be defined.
- `oint_s` E.dS = `q/ε_0` if charges of magnitude q were inside the surface.
Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region
- the electric field is necessarily zero.
- the electric field is due to the dipole moment of the charge distribution only.
- the dominant electric field is `∞ 1/r^3`, for large r, where r is the distance from a origin in this region.
- the work done to move a charged particle along a closed path, away from the region, will be zero.
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
