Advertisements
Advertisements
Question
State and explain Gauss’s law.
Solution
Gauss’s law states that the flux of the electric field through any closed surface S is 1/∈ₒ times the total charge enclosed by S
Let the total flux through a sphere of radius r enclose a point charge q at its centre. Divide the sphere into a small area element as shown in the figure.
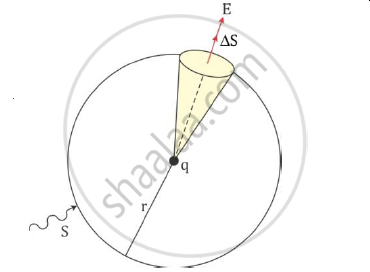
The flux through an area element ΔS is
`Deltaphi=E.DeltaS=q/(4piin_0r^2)hatr.DeltaS`
Here, we have used Coulomb’s law for the electric field due to a single charge q.
The unit vector `hatr`is along the radius vector from the centre to the area element. Because the normal to a sphere at every point is along the radius vector at that point, the area element ΔS and `hatr` have the same direction. Therefore
`Deltaphi=q/(4piin_0r^2)DeltaS`
Because the magnitude of the unit vector is 1, the total flux through the sphere is obtained by adding the flux through all the different area elements.
`phi=sum_(all DeltaS)q/(4piin_0r^2)DeltaS`
Because each area element of the sphere is at the same distance r from the charge,
`phi=q/(4piin_0r^2)sum_(all DeltaS)DeltaS=q/(4piin_0r^2)S`
Now, S the total area of the sphere equals 4πr². Thus,
`pi=q/(4piin_0r^2)xx4pir^2=q/in_0`
Hence, the above equation is a simple illustration of a general result of electrostatics called Gauss’s law
APPEARS IN
RELATED QUESTIONS
Gaussian surface cannot pass through discrete charge because ____________.
The surface considered for Gauss’s law is called ______.
The Electric flux through the surface
 (i) |
 (ii) |
 (iii) |
 (iv) |
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
If there were only one type of charge in the universe, then ______.
- `oint_s` E.dS ≠ 0 on any surface.
- `oint_s` E.dS = 0 if the charge is outside the surface.
- `oint_s` E.dS could not be defined.
- `oint_s` E.dS = `q/ε_0` if charges of magnitude q were inside the surface.
Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region
- the electric field is necessarily zero.
- the electric field is due to the dipole moment of the charge distribution only.
- the dominant electric field is `∞ 1/r^3`, for large r, where r is the distance from a origin in this region.
- the work done to move a charged particle along a closed path, away from the region, will be zero.
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
The region between two concentric spheres of radii a < b contain volume charge density ρ(r) = `"c"/"r"`, where c is constant and r is radial- distanct from centre no figure needed. A point charge q is placed at the origin, r = 0. Value of c is in such a way for which the electric field in the region between the spheres is constant (i.e. independent of r). Find the value of c:
In finding the electric field using Gauss law the formula `|vec"E"| = "q"_"enc"/(epsilon_0|"A"|)` is applicable. In the formula ε0 is permittivity of free space, A is the area of Gaussian surface and qenc is charge enclosed by the Gaussian surface. This equation can be used in which of the following situation?
