Advertisements
Advertisements
Question
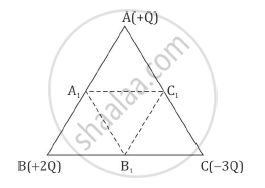
Three point charges, + Q + 2Q and – 3Q are placed at the vertices of an equilateral triangle ABC of side l. If these charges are displaced to the mid-point A1, B1 and C1, respectively, find the amount of the work done in shifting the charges to the new locations.
Advertisements
Solution
q1= +Q
q2= +2Q
q3= -3Q
r = l (for each side)
Intial potential energy of system
`U_1=1/(4piin_0l)[(q_1xxq_2)+(q_2xxq_3)+(q_3xxq_1)]`
`U_1=1/(4piin_0l)[(Qxx2Q)+(2Qxx(-3Q))+((-3Q) xxQ)]`
`U_1=(-7Q^2)/(4piin_0l`
These charges displaced to mid points then final potential energy of system,
`U_2=1/(4piin_0l/2)[(q_1xxq_2)+(q_2xxq_3)+(q_3xxq_1)]`
`U_2=2/(4piin_0l)[(Qxx2Q)+(2Qxx(-3Q))+((-3Q)xxQ)]`
`U_2=(-7Q^2)/(2piin_0l)`
Work done, W = U2 - U1
`W=(-7Q^2)/(2piin_0l)-(-7Q^2)/(4piin_0l)`
`W=(7Q^2)/(piin_0l)[(-1)/2-((-1)/4)]=(7Q^2)/(piin_0l)[(-1)/2+1/4]`
`W=(-7)/4(Q^2/(piin_0l))`
RELATED QUESTIONS
Obtain an expression for an intensity of electric field at a point at the end of position, i.e., the axial position of an electric dipole.
x
The electrostatic potential energy of two-point charges, 1 µC each, placed 1 meter apart in the air is:
Two point charges placed in a medium of dielectric constant 5 are at a distance r between them, experience an electrostatic force 'F'. The electrostatic force between them in vacuum at the same distance r will be-
If stretch in a spring of force constant k is tripled then the ratio of elastic potential energy in the two cases will be:
A work of 100 joule is performed in carrying a charge of 5 coulomb form infinity to a particular. point in an' electrostatic field. The potential of this point is:-
In bringing one electron towards another electrons, the electrostatic potential energy of the system will.
Three-point charges Q, q and -q are kept at the vertices of an equilateral triangle of side L as shown in the figure. What is
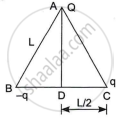
- the electrostatic potential energy of the arrangement? and
- the potential at point D?
An electric dipole with dipole moment 5 × 10−6 C m is aligned with the direction of a unifrom electric field of magnitude 4 × 105 N/C. The dipole is then rotated through an angle of 60° with respect to the electric field. The change in the potential energy of the dipole is ______.
