Advertisements
Advertisements
प्रश्न
State and explain Gauss’s law.
उत्तर
Gauss’s law states that the flux of the electric field through any closed surface S is 1/∈ₒ times the total charge enclosed by S
Let the total flux through a sphere of radius r enclose a point charge q at its centre. Divide the sphere into a small area element as shown in the figure.
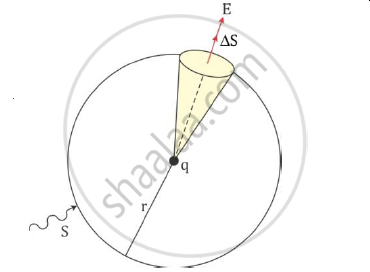
The flux through an area element ΔS is
`Deltaphi=E.DeltaS=q/(4piin_0r^2)hatr.DeltaS`
Here, we have used Coulomb’s law for the electric field due to a single charge q.
The unit vector `hatr`is along the radius vector from the centre to the area element. Because the normal to a sphere at every point is along the radius vector at that point, the area element ΔS and `hatr` have the same direction. Therefore
`Deltaphi=q/(4piin_0r^2)DeltaS`
Because the magnitude of the unit vector is 1, the total flux through the sphere is obtained by adding the flux through all the different area elements.
`phi=sum_(all DeltaS)q/(4piin_0r^2)DeltaS`
Because each area element of the sphere is at the same distance r from the charge,
`phi=q/(4piin_0r^2)sum_(all DeltaS)DeltaS=q/(4piin_0r^2)S`
Now, S the total area of the sphere equals 4πr². Thus,
`pi=q/(4piin_0r^2)xx4pir^2=q/in_0`
Hence, the above equation is a simple illustration of a general result of electrostatics called Gauss’s law
APPEARS IN
संबंधित प्रश्न
State Gauss’s law for magnetism. Explain its significance.
Answer the following question.
State Gauss's law for magnetism. Explain its significance.
q1, q2, q3 and q4 are point charges located at points as shown in the figure and S is a spherical gaussian surface of radius R. Which of the following is true according to the Gauss' law?

The Gaussian surface ______.
The surface considered for Gauss’s law is called ______.
Gauss' law helps in ______
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
The region between two concentric spheres of radii a < b contain volume charge density ρ(r) = `"c"/"r"`, where c is constant and r is radial- distanct from centre no figure needed. A point charge q is placed at the origin, r = 0. Value of c is in such a way for which the electric field in the region between the spheres is constant (i.e. independent of r). Find the value of c:
