Advertisements
Advertisements
प्रश्न
Answer the following question.
State Gauss's law for magnetism. Explain its significance.
उत्तर
The net magnetic flux (ΦB) through any closed surface is always zero.
This law suggests that the number of magnetic field lines leaving any closed surface is always equal to the number of magnetic field lines entering it.

Suppose a closed surface S is held in a uniform magnetic field `vecB`.
Consider a small vector area element Δ`vec"S"` of this surface.
Magnetic flux through this area element is defined as ΔΦB = `vec"B".Δvec"S" `
Considering all small area elements of the surface, we obtain net magnetic flux through the surface as:
ØB = `sum_"All" ΔØ_"B" = sum_"All" vec"B". Δvec"S" = 0`
APPEARS IN
संबंधित प्रश्न
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
Gaussian surface cannot pass through discrete charge because ____________.
Gauss' law helps in ______
The Electric flux through the surface
 (i) |
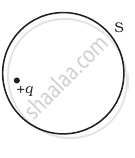 (ii) |
 (iii) |
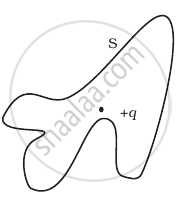 (iv) |
Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region
- the electric field is necessarily zero.
- the electric field is due to the dipole moment of the charge distribution only.
- the dominant electric field is `∞ 1/r^3`, for large r, where r is the distance from a origin in this region.
- the work done to move a charged particle along a closed path, away from the region, will be zero.
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
The region between two concentric spheres of radii a < b contain volume charge density ρ(r) = `"c"/"r"`, where c is constant and r is radial- distanct from centre no figure needed. A point charge q is placed at the origin, r = 0. Value of c is in such a way for which the electric field in the region between the spheres is constant (i.e. independent of r). Find the value of c:
