Advertisements
Advertisements
Question
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
Options
E on the LHS of the above equation will have a contribution from q1, q5 and q3 while q on the RHS will have a contribution from q2 and q4 only.
E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only.
E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q1, q3 and q5 only.
Both E on the LHS and q on the RHS will have contributions from q2 and q4 only.
Solution
E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only.
Explanation:
According to Gauss’ law, the term `q_(enclosed)` on the right side of the equation `oint_s E.ds = q_(enclosed)/ε_0` includes the sum of all charges enclosed by the surface called (Gaussian surface). In left side equation, the electric field is due to all the charges present both inside as well as outside the Gaussian surface.
APPEARS IN
RELATED QUESTIONS
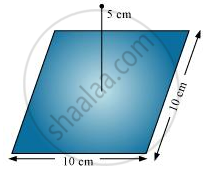
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
A thin conducting spherical shell of radius R has charge Q spread uniformly over its surface. Using Gauss’s law, derive an expression for an electric field at a point outside the shell.
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0 ≤ r ≤ ∞.
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
Gauss' law helps in ______
If there were only one type of charge in the universe, then ______.
- `oint_s` E.dS ≠ 0 on any surface.
- `oint_s` E.dS = 0 if the charge is outside the surface.
- `oint_s` E.dS could not be defined.
- `oint_s` E.dS = `q/ε_0` if charges of magnitude q were inside the surface.
Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then
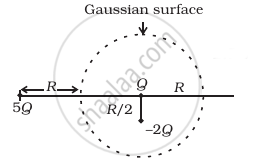
- total flux through the surface of the sphere is `(-Q)/ε_0`.
- field on the surface of the sphere is `(-Q)/(4 piε_0 R^2)`.
- flux through the surface of sphere due to 5Q is zero.
- field on the surface of sphere due to –2Q is same everywhere.
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
