Advertisements
Advertisements
Question
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
Solution
By using Gauss’s Law.
It is given as
`Phi = oint vecE*dvecs = q/in_0`
Now, the flux passing through all the six surfaces would be
`Phi = 6phi =q/in_0`
And the flux passing through each surface would be
`phi = q/(6in_0)`
RELATED QUESTIONS
State and explain Gauss’s law.
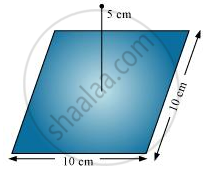
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
Gaussian surface cannot pass through discrete charge because ____________.
q1, q2, q3 and q4 are point charges located at points as shown in the figure and S is a spherical gaussian surface of radius R. Which of the following is true according to the Gauss' law?

The Gaussian surface ______.
Gauss' law helps in ______
The Electric flux through the surface
 (i) |
 (ii) |
 (iii) |
 (iv) |
Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then
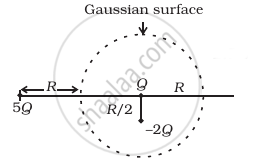
- total flux through the surface of the sphere is `(-Q)/ε_0`.
- field on the surface of the sphere is `(-Q)/(4 piε_0 R^2)`.
- flux through the surface of sphere due to 5Q is zero.
- field on the surface of sphere due to –2Q is same everywhere.
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
