Advertisements
Advertisements
प्रश्न
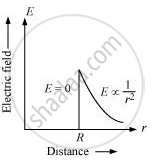
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0 ≤ r ≤ ∞.
उत्तर
The graph of electric field E(r) with distance r from the centre of the shell for 0 ≤ r ≤ ∞.
APPEARS IN
संबंधित प्रश्न
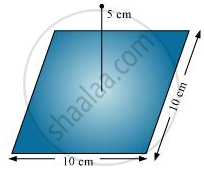
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
A thin conducting spherical shell of radius R has charge Q spread uniformly over its surface. Using Gauss’s law, derive an expression for an electric field at a point outside the shell.
State Gauss's law in electrostatics. Show, with the help of a suitable example along with the figure, that the outward flux due to a point charge 'q'. in vacuum within a closed surface, is independent of its size or shape and is given by `q/ε_0`
Answer the following question.
State Gauss's law on electrostatics and drive expression for the electric field due to a long straight thin uniformly charged wire (linear charge density λ) at a point lying at a distance r from the wire.
q1, q2, q3 and q4 are point charges located at points as shown in the figure and S is a spherical gaussian surface of radius R. Which of the following is true according to the Gauss' law?

The Gaussian surface ______.
If the total charge enclosed by a surface is zero, does it imply that the elecric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
