Advertisements
Advertisements
प्रश्न
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
उत्तर
According to Gauss' law, the electric flux through an enclosed surface is given by `oint_s vecE * dvecS = q_(enclosed)/ε_0`.
The net charge on a dipole is given by –q + q = 0, hence `q_(enclosed)` = 0
Hence the electric flux through a surface enclosing a dipole = `(-q + q)/ε_0 = q/ε_0` = 0
APPEARS IN
संबंधित प्रश्न
State and explain Gauss’s law.
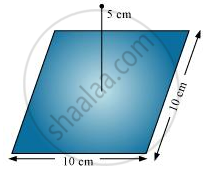
A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in the Figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
State Gauss’s law for magnetism. Explain its significance.
Which of the following statements is not true about Gauss’s law?
Gauss' law helps in ______
Five charges q1, q2, q3, q4, and q5 are fixed at their positions as shown in figure. S is a Gaussian surface. The Gauss’s law is given by `oint_s E.ds = q/ε_0`
Which of the following statements is correct?
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: ep = – (1 + y)e where e is the electronic charge.
- Find the critical value of y such that expansion may start.
- Show that the velocity of expansion is proportional to the distance from the centre.
A charge Q is placed at the centre of a cube. The electric flux through one of its faces is ______.
