Advertisements
Advertisements
प्रश्न
A constant current exists in an inductor-coil connected to a battery. The coil is short-circuited and the battery is removed. Show that the charge flown through the coil after the short-circuiting is the same as that which flows in one time constant before the short-circuiting.
उत्तर
Consider an inductance L, a resitance R and a source of emf `xi` are connected in series.
Time constant of this LR circuit is,
`tau=L/R`
let a constant current `(i_0=xi/R)` is maitened in the circuit before removal of the battery.
Charge flown in one time constant before the short-circuiting is,
\[Q_\tau = i_0 \tau..........(1)\]
Discahrge equation for LR circuit after short circuiting is given as,
\[i = i_0 e^{- \frac{t}{\tau}}\]
Change flown from the inductor in small time dt after the short circuiting is given as,
dQ = idt
Chrage flown from the inductor after short circuting can be found by interating the above eqation within the proper limits of time,
\[Q = \int_0^\infty idt\]
\[ \Rightarrow Q = \int_0^\infty i_0 e^{- \frac{t}{\tau}} dt\]
\[ \Rightarrow Q = \left[ - \tau i_0 e^{- \frac{t}{\tau}} \right]_0^\infty \]
\[ \Rightarrow Q = - \tau i_0 \left[ 0 - 1 \right]\]
\[ \Rightarrow Q = \tau i_0 ............. (2)\]
Hence, proved.
APPEARS IN
संबंधित प्रश्न
In a series LCR circuit connected to an a.c. source of voltage v = vmsinωt, use phasor diagram to derive an expression for the current in the circuit. Hence, obtain the expression for the power dissipated in the circuit. Show that power dissipated at resonance is maximum
A series LCR circuit is connected across an a.c. source of variable angular frequency 'ω'. Plot a graph showing variation of current 'i' as a function of 'ω' for two resistances R1 and R2 (R1 > R2).
Answer the following questions using this graph :
(a) In which case is the resonance sharper and why?
(b) In which case in the power dissipation more and why?
An LR circuit contains an inductor of 500 mH, a resistor of 25.0 Ω and an emf of 5.00 V in series. Find the potential difference across the resistor at t = (a) 20.0 ms, (b) 100 ms and (c) 1.00 s.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
An ac circuit as shown in the figure has an inductor of inductance L and a resistor or resistance R connected in series. Using the phasor diagram, explain why the voltage in the circuit will lead the current in phase.
Answer the following question.
Draw the diagram of a device that is used to decrease high ac voltage into a low ac voltage and state its working principle. Write four sources of energy loss in this device.
Using the phasor diagram, derive the expression for the current flowing in an ideal inductor connected to an a.c. source of voltage, v= vo sin ωt. Hence plot graphs showing the variation of (i) applied voltage and (ii) the current as a function of ωt.
Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements, L, C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified for this frequency.
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
The resonant frequency of a RF oscillator is 1 MHz and its bandwidth is 10 kHz. The quality factor will be :
To reduce the resonant frequency in an LCR series circuit with a generator
Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
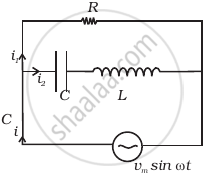
Define Impedance.
When an alternating voltage of 220V is applied across device X, a current of 0.25A flows which lags behind the applied voltage in phase by π/2 radian. If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
- Name the devices X and Y.
- Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
Select the most appropriate option with regard to resonance in a series LCR circuit.
Three students, X, Y and Z performed an experiment for studying the variation of a.c. with frequency in a series LCR circuit and obtained the graphs as shown below. They all used
- an AC source of the same emf and
- inductance of the same value.
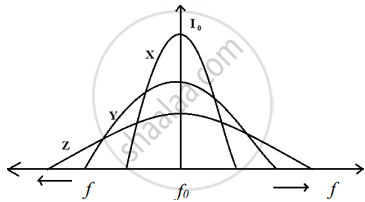
- Who used minimum resistance?
- In which case will the quality Q factor be maximum?
- What did the students conclude about the nature of impedance at resonant frequency (f0)?
- An ideal capacitor is connected across 220V, 50Hz, and 220V, 100Hz supplies. Find the ratio of current flowing through it in the two cases.
