Advertisements
Advertisements
प्रश्न
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
उत्तर
Consider L-C-R series circuit with AC supply
V = Vm sin ωt
Applying voltage Kirchhoff's law over the circuit
∴ VL + VC + VR = Vm sin ωt
L = `(di)/(dt) + Ri + q/c` = Vi = Vm sin ωt
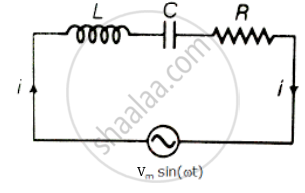
Multiply the above equation by i on both the sides.
L = `(di)/(dt) + Ri + q/c` = Vi = Vm sin ωt
Multiply the above equation by `1/2` on both sides
`1/2 Li (di)/(dt) + i q/(2C) + (i^2R)/2 = 1/2` Vmi sin ωt `(∵ i = (dq)/(dt))`
`(d(1/2 Li^2))/(dt) + 1/(2C) (dq^2)/(dt) + (i^2R)/2 = 1/2` Vmi sin ωt .....(I)
(i) `(d(1/2 li^2))/(dt)` Represents the rate of change of potential energy in inductance L.
(ii) `d/(dt) q^2/(2C)` represents energy stored in dt time in the capacitor.
(iii) i2R represents joules heating loss.
(iv) `1/2 V_m i` sin ωt is the rate at which driving force pours in energy. It goes into ohmic loss and increase of stored energy in capacitor and inductor.
Vi = rate at which driving force pours in energy. It goes into (i) ohmic loss and (ii) increase of stored energy.
Hence equation (ii) is in the form of conservation of energy statement. Integrating both sides of equation. (ii) with respect to time over one full cycle (0 → T) we may write
`int_0^T d/(dt) (1/2 Li^2 + q^2/(2C)) dt + int_0^T Ri^2 dt = int_0^T Vi dt`
⇒ 0 + (+ ve) = `int_0^T Vi dt`
⇒ `int_0^T Vi dt > 0` if phase difference between V and i is a constant and acute angle.
APPEARS IN
संबंधित प्रश्न
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
Two coils A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10 Ω. Each coil is connected to an ideal battery of emf 2.0 V at t = 0. Let iA and iBbe the currents in the two circuit at time t. Find the ratio iA / iB at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1 s.
Use the expression for Lorentz force acting on the charge carriers of a conductor to obtain the expression for the induced emf across the conductor of length l moving with velocity v through a magnetic field B acting perpendicular to its length.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
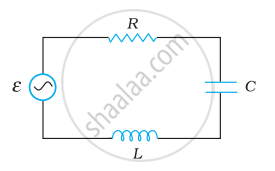
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
Obtain the resonant frequency and Q-factor of a series LCR circuit with L = 3.0 H, C = 27 µF, and R = 7.4 Ω. It is desired to improve the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way.
Assertion: When the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero, and so there is no current through the inductor or the capacitor.
Reason: The net current in the inductor and capacitor is zero.
To reduce the resonant frequency in an LCR series circuit with a generator ______.
An alternating voltage of 220 V is applied across a device X. A current of 0.22 A flows in the circuit and it lags behind the applied voltage in phase by π/2 radian. When the same voltage is applied across another device Y, the current in the circuit remains the same and it is in phase with the applied voltage.
- Name the devices X and Y and,
- Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
