Question

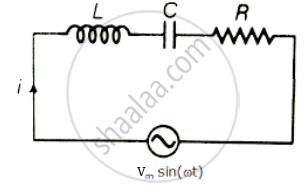
In the LCR circuit shown in figure, the ac driving voltage is v = v_m sin ωt.

1. Write down the equation of motion for q (t).
2. At t = t₀, the voltage source stops and R is short circuited. Now write down how much energy is stored in each of L and C.
3. Describe subsequent motion of charges.

Answer 1

i. Consider series LCR circuit and tapping key K to short circuit R. Let i be the current in circuit. Then by Kirchhoff's voltage law, when key K is open.

V_R+ V_L + V_C = V_m sin ωt

`iR + L (di(t))/(dt) + (q(t))/C - V_m` sin ωt = 0  .....[∵ i(t) = i = l_m sin[ωt + `phi`]

⇒ As charge q(t) changes in circuit with time in AC,

Then `i = (dq(t))/(dt)`

`(di)/(dt) = (d^2q(t))/(dt^2)`    .....(Differentiating again)

`R (dq(t))/(dt) + L (d^2q(t))/(dt^2) + (q(t))/C = V_m` sin ωt

`L (d^2q(t))/(dt) + R (dq(t))/(dt) + (q(t))/C = V_m` sin ωt

This is the equation for variation of motion of charge with respect to time.

ii. Let time-dependent charge in circuit is at phase angle with voltage then q = q_m cos (ωt + `phi`)

i = `(dq)/(dt) = ω q_m sin (ωt + phi)`  ......(I)

`i_m = V_m/Z = V_m/sqrt(R^2 + (X_C - X_L)^2)`  ......(II)

`tan phi = (X_C - X_L)/R`

At t = t₀, R is short-circuited, then energy stored in L and C, when K is closed will be, `U_L = 1/2 Li`  ......(III)

At t = t₀

i = i_m sin (ωt₀ + `phi`)  ......(IV)

From (II)

`i = V_m/sqrt(R^2 + (X_C - X_L)^2) sin (ωt_0 + phi)`  ......(V)

∴ U_L = `1/2[V_m/sqrt(R^2 + (X_C - X_L)^2]]^2 sin^2(ωt_0 + phi)`

U_C = `q^2/(2C) = 1/(2C) [q_m^2  cos^2 (ωt_0 + pji)]`

Comparing (IV) and (I) I_m = q_mω

∴ `q_m = i_m/ω`

∴ U_C = `1/(2C) * (i_m^2)/ω^2 cos^2 (ωt_0 + phi) = (i_m^2)/(2Cω^2) cos^2 (ωt_0 + phi)`

Using equation (II)

U_C = `1/(2Cω^2) [(V_m^2)/(R^2 + (X_C - X_L)^2)]^2 cos^2 (ωt_0 + phi)`

iii. When R is short-circuited, the circuit becomes L-C oscillator. The capacitor will go discharging and all energy will transfer to L and back and forth. Hence there is oscillation of energy from electrostatic to magnetic and vice versa.