Advertisements
Advertisements
Question
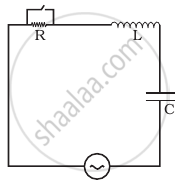
In the LCR circuit shown in figure, the ac driving voltage is v = vm sin ωt.
- Write down the equation of motion for q (t).
- At t = t0, the voltage source stops and R is short circuited. Now write down how much energy is stored in each of L and C.
- Describe subsequent motion of charges.
Solution
i. Consider series LCR circuit and tapping key K to short circuit R. Let i be the current in circuit. Then by Kirchhoff's voltage law, when key K is open.
VR+ VL + VC = Vm sin ωt
`iR + L (di(t))/(dt) + (q(t))/C - V_m` sin ωt = 0 .....[∵ i(t) = i = lm sin[ωt + `phi`]
⇒ As charge q(t) changes in circuit with time in AC,
Then `i = (dq(t))/(dt)`
`(di)/(dt) = (d^2q(t))/(dt^2)` .....(Differentiating again)
`R (dq(t))/(dt) + L (d^2q(t))/(dt^2) + (q(t))/C = V_m` sin ωt
`L (d^2q(t))/(dt) + R (dq(t))/(dt) + (q(t))/C = V_m` sin ωt
This is the equation for variation of motion of charge with respect to time.
ii. Let time-dependent charge in circuit is at phase angle with voltage then q = qm cos (ωt + `phi`)
i = `(dq)/(dt) = ω q_m sin (ωt + phi)` ......(I)
`i_m = V_m/Z = V_m/sqrt(R^2 + (X_C - X_L)^2)` ......(II)
`tan phi = (X_C - X_L)/R`
At t = t0, R is short-circuited, then energy stored in L and C, when K is closed will be, `U_L = 1/2 Li` ......(III)
At t = t0
i = im sin (ωt0 + `phi`) ......(IV)
From (II)
`i = V_m/sqrt(R^2 + (X_C - X_L)^2) sin (ωt_0 + phi)` ......(V)
∴ UL = `1/2[V_m/sqrt(R^2 + (X_C - X_L)^2]]^2 sin^2(ωt_0 + phi)`
UC = `q^2/(2C) = 1/(2C) [q_m^2 cos^2 (ωt_0 + pji)]`
Comparing (IV) and (I) Im = qmω
∴ `q_m = i_m/ω`
∴ UC = `1/(2C) * (i_m^2)/ω^2 cos^2 (ωt_0 + phi) = (i_m^2)/(2Cω^2) cos^2 (ωt_0 + phi)`
Using equation (II)
UC = `1/(2Cω^2) [(V_m^2)/(R^2 + (X_C - X_L)^2)]^2 cos^2 (ωt_0 + phi)`
iii. When R is short-circuited, the circuit becomes L-C oscillator. The capacitor will go discharging and all energy will transfer to L and back and forth. Hence there is oscillation of energy from electrostatic to magnetic and vice versa.
APPEARS IN
RELATED QUESTIONS
When an AC source is connected to a capacitor, there is a steady-state current in the circuit. Does it mean that the charges jump from one plate to the other to complete the circuit?
The AC voltage across a resistance can be measured using
The dielectric strength of air is 3.0 × 106 V/m. A parallel-plate air-capacitor has area 20 cm2 and plate separation 0.10 mm. Find the maximum rms voltage of an AC source that can be safely connected to this capacitor.
A transformer has 50 turns in the primary and 100 in the secondary. If the primary is connected to a 220 V DC supply, what will be the voltage across the secondary?
Compare resistance and reactance.
A device Y is connected across an AC source of emf e = e0 sin ωt. The current through Y is given as i = i0 sin (ωt + π/2).
- Identify the device Y and write the expression for its reactance.
- Draw graphs showing a variation of emf and current with time over one cycle of AC for Y.
- How does the reactance of the device Y vary with the frequency of the AC? Show graphically.
- Draw the phasor diagram for device Y.
Average power supplied to a capacitor over one complete cycle is ______.
A.C. power is transmitted from a power house at a high voltage as ______.
When an ac voltage of 220 V is applied to the capacitor C, then ______.
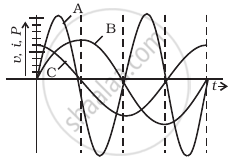
A device ‘X’ is connected to an a.c source. The variation of voltage, current and power in one complete cycle is shown in figure.
- Which curve shows power consumption over a full cycle?
- What is the average power consumption over a cycle?
- Identify the device ‘X’.