Advertisements
Advertisements
प्रश्न
Two coils A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10 Ω. Each coil is connected to an ideal battery of emf 2.0 V at t = 0. Let iA and iBbe the currents in the two circuit at time t. Find the ratio iA / iB at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1 s.
उत्तर
Given:-
Inductance of the coil A, LA = 1.0 H
Inductance of the coil B, LB = 2.0 H
Resistance in each coil, R = 10 Ω
The current in the LR circuit after t seconds after connecting the battery is given by
i = i0 (1 − e−t/τ)
Here,
i0 = Steady state current
τ = Time constant = `L/R`
(a) At t = 0.1 s, time constants of the coils A and B are τA and τB, respectively.
Now,
\[\tau_A = \frac{1}{10} = 0 . 1 s\]
\[ \tau_B = \frac{2}{10} = 0 . 2 s\]
Currents in the coils can be calculated as follows:-
\[i_A = i_0 (1 - e^{- t/\tau} ), \]
\[ = \frac{2}{10}\left( 1 - e^\frac{0 . 1 \times 10}{1} \right) = 0 . 2 (1 - e^{- 1} )\]
\[ = 0 . 126424111\]
\[ i_B = i_0 (1 - e^{- t/\tau} )\]
\[ = \frac{2}{10}(1 - e^{0 . 1 \times 10/2} )\]
\[ = 0 . 2 (1 - e^{- 1/2} ) = 0 . 078693\]
\[\therefore \frac{i_A}{i_B} = \frac{0 . 126411}{0 . 78693} = 1 . 6\]
(b) At t = 200 ms = 0.2 s,
iA = 0.2 (1 − e−0.2 × 10.1)
iA = 0.2 × 0.864664716
iA = 0.1729329943
iB = 0.2 (1 − e−0.2 × 10.2)
iB = 0.2 × 0.632120 = 0.126424111
\[\therefore \frac{i_A}{i_B} = \frac{0 . 172932343}{0 . 126424111} = 1 . 36 = 1 . 4\]
(c) At time t = 1 s,
iA = 0.2 (1 − e−1 × 10.1)
= 0.2 − 0.9999549
= 0.19999092
iB = 0.2 (1 − e−1 × 10.2)
= 0.2 × 0.99326 = 0.19865241
\[\therefore \frac{i_A}{i_B} = \frac{0 . 19999092}{0 . 19999092} \approx 1 . 0\]
APPEARS IN
संबंधित प्रश्न
In a series LCR circuit, VL = VC ≠ VR. What is the value of power factor?
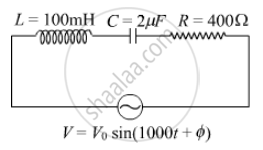
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?
(ii) Without making any other change, find the value of the additional capacitor C1, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
Derive an expression for the average power consumed in a series LCR circuit connected to a.c. source in which the phase difference between the voltage and the current in the circuit is Φ.
The current in a discharging LR circuit without the battery drops from 2.0 A to 1.0 A in 0.10 s. (a) Find the time constant of the circuit. (b) If the inductance of the circuit 4.0 H, what is its resistance?
(i) An a.c. source of emf ε = 200 sin omegat is connected to a resistor of 50 Ω . calculate :
(1) Average current (`"I"_("avg")`)
(2) Root mean square (rms) value of emf
(ii) State any two characteristics of resonance in an LCR series circuit.
Choose the correct answer from given options
The phase difference between the current and the voltage in series LCR circuit at resonance is
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 µF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
Obtain the resonant frequency and Q-factor of a series LCR circuit with L = 3.0 H, C = 27 µF, and R = 7.4 Ω. It is desired to improve the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way.
In series LCR circuit, the phase angle between supply voltage and current is ______.
The resonant frequency of a RF oscillator is 1 MHz and its bandwidth is 10 kHz. The quality factor will be :
In series LCR AC-circuit, the phase angle between current and voltage is
To reduce the resonant frequency in an LCR series circuit with a generator ______.
Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
As the frequency of an ac circuit increases, the current first increases and then decreases. What combination of circuit elements is most likely to comprise the circuit?
- Inductor and capacitor.
- Resistor and inductor.
- Resistor and capacitor.
- Resistor, inductor and capacitor.
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
Draw a labelled graph showing variation of impedance (Z) of a series LCR circuit Vs frequency (f) of the ac supply. Mark the resonant frequency as f0·
