Advertisements
Advertisements
प्रश्न
As the frequency of an ac circuit increases, the current first increases and then decreases. What combination of circuit elements is most likely to comprise the circuit?
- Inductor and capacitor.
- Resistor and inductor.
- Resistor and capacitor.
- Resistor, inductor and capacitor.
पर्याय
a and b
b and c
c and d
a and d
उत्तर
a and d
Explanation:
Compare the given circuit by predicting the variation in their reactances with frequency. So, that then we can decide the elements.
Reactance of an inductor of inductance L is XL = 2πvL, where v is the frequency of the AC circuit.
XC = Reactance of the capacitive circuit = `1/(2pi fC)`
With an increase in frequency `(f)` of an AC circuit, R remains constant, inductive reactance (XL) increases and capacitive reactance (XC) decreases.
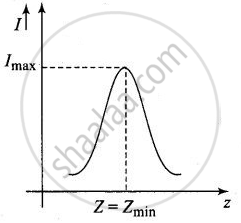
For an L-C-R circuit,
Z = Impedance of the circuit
= `sqrt(R^2 + (X_L - X_C)^2)`
= `sqrt(R^2 + (2pivL - 1/(2pivC)^2)`
As frequency (v) increases, Z decreases and at certain value of the frequency known as resonant frequency (v0), impedance Z is minimum that is Zmin = R current varies inversely with impedance and at Zmin current is maximum.
APPEARS IN
संबंधित प्रश्न
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
An LR circuit contains an inductor of 500 mH, a resistor of 25.0 Ω and an emf of 5.00 V in series. Find the potential difference across the resistor at t = (a) 20.0 ms, (b) 100 ms and (c) 1.00 s.
A constant current exists in an inductor-coil connected to a battery. The coil is short-circuited and the battery is removed. Show that the charge flown through the coil after the short-circuiting is the same as that which flows in one time constant before the short-circuiting.
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
If an LCR series circuit is connected to an ac source, then at resonance the voltage across ______.
The resonant frequency of a RF oscillator is 1 MHz and its bandwidth is 10 kHz. The quality factor will be :
To reduce the resonant frequency in an LCR series circuit with a generator ______.
A coil of 0.01 henry inductance and 1 ohm resistance is connected to 200 volt, 50 Hz ac supply. Find the impedance of the circuit and time lag between max. alternating voltage and current.
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit.
