Advertisements
Advertisements
प्रश्न
Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
पर्याय
R = 20 Ω, L = 1.5 H, C = 35µF.
R = 25 Ω, L = 2.5 H, C = 45µF.
R = 15 Ω, L = 3.5 H, C = 30µF.
R = 25 Ω, L = 1.5 H, C = 45µF.
उत्तर
R = 15 Ω, L = 3.5 H, C = 30µF.
Explanation:
Quality factor (Q-factor) of the series resonant circuit:
(i) The characteristic of a series resonant circuit is determined by the quality factor (Q-factor) of the circuit.
(ii) It defines sharpness if i - v curve at resonance when Q-factor is large, the sharpness of resonance curve is more and vice-versa.
(iii) Q-factor is also defined as follows:
Q-factor = `2pi xx "Max energy stored"/"Energy dissipation"`
= `(2pi)/T xx "Max energy stored"/"Mean power dissipated"`
= `"Resonant frequency"/"Bandwidth" = ω_0/(Δω)`
(iv) Q-factor = `V_L/V_R` or `V_C/V_R = (ω_0L)/R` or `1/(ω_0CR)`
⇒ Q-factor = `1/R sqrt(L/C)`
For better tuning of an L-C-R circuit used for communication, quality factor of the circuit must be as high as possible.
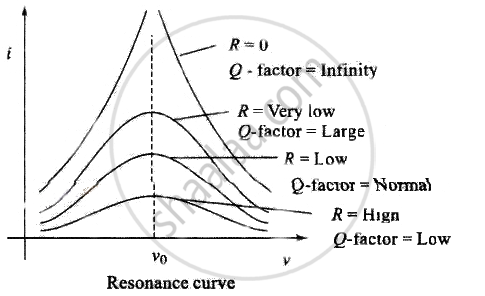
We know quality factor should be high for better tuning.
Quality factor (Q) of an L-C-R circuit is `Q = 1/R sqrt(L/C)`
Where R is the resistance, L is the inductance and C is the capacitance of the circuit.
For high Q factor R should be low, L should be high and C should be low.
Important point: Be careful while writing formula for quality factor, this formula we used in this case is only for series L-C-R circuit.
APPEARS IN
संबंधित प्रश्न
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
An L-R circuit has L = 1.0 H and R = 20 Ω. It is connected across an emf of 2.0 V at t = 0. Find di/dt at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1.0 s.
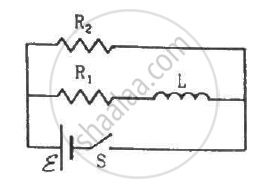
Consider the circuit shown in figure. (a) Find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c) Find the current through the inductor after one time constant.
Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements, L, C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified for this frequency.
In series combination of R, L and C with an A.C. source at resonance, if R = 20 ohm, then impedence Z of the combination is ______.
The resonant frequency of a RF oscillator is 1 MHz and its bandwidth is 10 kHz. The quality factor will be :
An alternating voltage of 220 V is applied across a device X. A current of 0.22 A flows in the circuit and it lags behind the applied voltage in phase by π/2 radian. When the same voltage is applied across another device Y, the current in the circuit remains the same and it is in phase with the applied voltage.
- Name the devices X and Y and,
- Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
Draw the impedance triangle for a series LCR AC circuit and write the expressions for the impedance and the phase difference between the emf and the current.
Draw a labelled graph showing variation of impedance (Z) of a series LCR circuit Vs frequency (f) of the ac supply. Mark the resonant frequency as f0·
Three students, X, Y and Z performed an experiment for studying the variation of a.c. with frequency in a series LCR circuit and obtained the graphs as shown below. They all used
- an AC source of the same emf and
- inductance of the same value.
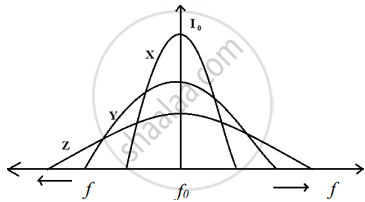
- Who used minimum resistance?
- In which case will the quality Q factor be maximum?
- What did the students conclude about the nature of impedance at resonant frequency (f0)?
- An ideal capacitor is connected across 220V, 50Hz, and 220V, 100Hz supplies. Find the ratio of current flowing through it in the two cases.
