Advertisements
Advertisements
Question
Two coils A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10 Ω. Each coil is connected to an ideal battery of emf 2.0 V at t = 0. Let iA and iBbe the currents in the two circuit at time t. Find the ratio iA / iB at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1 s.
Solution
Given:-
Inductance of the coil A, LA = 1.0 H
Inductance of the coil B, LB = 2.0 H
Resistance in each coil, R = 10 Ω
The current in the LR circuit after t seconds after connecting the battery is given by
i = i0 (1 − e−t/τ)
Here,
i0 = Steady state current
τ = Time constant = `L/R`
(a) At t = 0.1 s, time constants of the coils A and B are τA and τB, respectively.
Now,
\[\tau_A = \frac{1}{10} = 0 . 1 s\]
\[ \tau_B = \frac{2}{10} = 0 . 2 s\]
Currents in the coils can be calculated as follows:-
\[i_A = i_0 (1 - e^{- t/\tau} ), \]
\[ = \frac{2}{10}\left( 1 - e^\frac{0 . 1 \times 10}{1} \right) = 0 . 2 (1 - e^{- 1} )\]
\[ = 0 . 126424111\]
\[ i_B = i_0 (1 - e^{- t/\tau} )\]
\[ = \frac{2}{10}(1 - e^{0 . 1 \times 10/2} )\]
\[ = 0 . 2 (1 - e^{- 1/2} ) = 0 . 078693\]
\[\therefore \frac{i_A}{i_B} = \frac{0 . 126411}{0 . 78693} = 1 . 6\]
(b) At t = 200 ms = 0.2 s,
iA = 0.2 (1 − e−0.2 × 10.1)
iA = 0.2 × 0.864664716
iA = 0.1729329943
iB = 0.2 (1 − e−0.2 × 10.2)
iB = 0.2 × 0.632120 = 0.126424111
\[\therefore \frac{i_A}{i_B} = \frac{0 . 172932343}{0 . 126424111} = 1 . 36 = 1 . 4\]
(c) At time t = 1 s,
iA = 0.2 (1 − e−1 × 10.1)
= 0.2 − 0.9999549
= 0.19999092
iB = 0.2 (1 − e−1 × 10.2)
= 0.2 × 0.99326 = 0.19865241
\[\therefore \frac{i_A}{i_B} = \frac{0 . 19999092}{0 . 19999092} \approx 1 . 0\]
APPEARS IN
RELATED QUESTIONS
Define 'quality factor' of resonance in a series LCR circuit. What is its SI unit?
In a series LCR circuit connected to an a.c. source of voltage v = vmsinωt, use phasor diagram to derive an expression for the current in the circuit. Hence, obtain the expression for the power dissipated in the circuit. Show that power dissipated at resonance is maximum
In a series LCR circuit, obtain the condition under which watt-less current flows in the circuit ?
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
Derive an expression for the average power consumed in a series LCR circuit connected to a.c. source in which the phase difference between the voltage and the current in the circuit is Φ.
An LR circuit contains an inductor of 500 mH, a resistor of 25.0 Ω and an emf of 5.00 V in series. Find the potential difference across the resistor at t = (a) 20.0 ms, (b) 100 ms and (c) 1.00 s.
A solenoid having inductance 4.0 H and resistance 10 Ω is connected to a 4.0 V battery at t = 0. Find (a) the time constant, (b) the time elapsed before the current reaches 0.63 of its steady-state value, (c) the power delivered by the battery at this instant and (d) the power dissipated in Joule heating at this instant.
A constant current exists in an inductor-coil connected to a battery. The coil is short-circuited and the battery is removed. Show that the charge flown through the coil after the short-circuiting is the same as that which flows in one time constant before the short-circuiting.
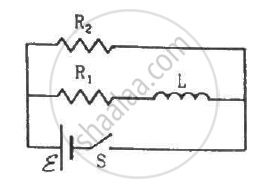
Consider the circuit shown in figure. (a) Find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c) Find the current through the inductor after one time constant.
The potential difference across the resistor is 160V and that across the inductor is 120V. Find the effective value of the applied voltage. If the effective current in the circuit be 1.0 A, calculate the total impedance of the circuit.
In a series, LCR circuit, obtain an expression for the resonant frequency,
Derive an expression for the average power dissipated in a series LCR circuit.
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 µF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
For a series LCR-circuit, the power loss at resonance is ______.
At resonant frequency the current amplitude in series LCR circuit is ______.
The resonant frequency of a RF oscillator is 1 MHz and its bandwidth is 10 kHz. The quality factor will be :
If the rms current in a 50 Hz ac circuit is 5 A, the value of the current 1/300 seconds after its value becomes zero is ______.
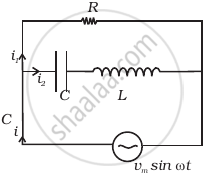
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
Draw a labelled graph showing variation of impedance (Z) of a series LCR circuit Vs frequency (f) of the ac supply. Mark the resonant frequency as f0·
