Advertisements
Advertisements
Question
The current in a discharging LR circuit without the battery drops from 2.0 A to 1.0 A in 0.10 s. (a) Find the time constant of the circuit. (b) If the inductance of the circuit 4.0 H, what is its resistance?
Solution
The current in the discharging LR circuit after t seconds is given by
i = i0 e−t/τ
Here,
i0 = Steady state current = 2 A
Now, let the time constant be τ.
In time t = 0.10 s, the current drops to 1 A.
\[i = i_0 \left( 1 - e^{- t/\tau} \right)\]
\[ \Rightarrow 1 = 2\left( 1 - e^{- t/\tau} \right)\]
\[ \Rightarrow \frac{1}{2} = 1 - e^{- t/\tau} \]
\[ \Rightarrow e^{- t/\tau} = 1 - \frac{1}{2}\]
\[ \Rightarrow e^{- t/\tau} = \frac{1}{2}\]
\[ \Rightarrow \ln\left( e^{- t/\tau} \right) = \ln\left( \frac{1}{2} \right) = \]
\[ \Rightarrow - \frac{0 . 1}{\tau} = - 0 . 693\]
The time constant is given by
\[\tau = \frac{0 . 1}{0 . 693} = 0 . 144 = 0 . 14\]
(b) Given:-
Inductance in the circuit, L = 4 H
Let the resistance in the circuit be R.
The time constant is given by
\[\tau = \frac{L}{R}\]
From the above relation, we have
\[0 . 14 = \frac{4}{R}\]
\[ \Rightarrow R = \frac{4}{0 . 14}\]
\[ \Rightarrow R = 28 . 5728 \Omega\]
APPEARS IN
RELATED QUESTIONS
Why does current in a steady state not flow in a capacitor connected across a battery? However momentary current does flow during charging or discharging of the capacitor. Explain.
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
Show that in an a.c. circuit containing a pure inductor, the voltage is ahead of current by π/2 in phase ?
Derive an expression for the average power consumed in a series LCR circuit connected to a.c. source in which the phase difference between the voltage and the current in the circuit is Φ.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
Two coils A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10 Ω. Each coil is connected to an ideal battery of emf 2.0 V at t = 0. Let iA and iBbe the currents in the two circuit at time t. Find the ratio iA / iB at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1 s.
What will be the potential difference in the circuit when direct current is passed through the circuit?
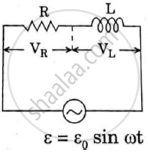
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
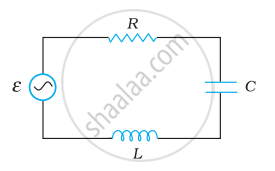
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
In series combination of R, L and C with an A.C. source at resonance, if R = 20 ohm, then impedence Z of the combination is ______.
In series LCR circuit, the phase angle between supply voltage and current is ______.
A series LCR circuit containing a 5.0 H inductor, 80 µF capacitors, and 40 Ω resistor is connected to a 230 V variable frequency ac source. The angular frequencies of the source at which power is transferred to the circuit are half the power at the resonant angular frequency are likely to be ______.
To reduce the resonant frequency in an LCR series circuit with a generator ______.
Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
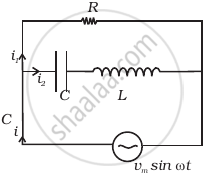
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
Which of the following statements about a series LCR circuit connected to an ac source is correct?
Select the most appropriate option with regard to resonance in a series LCR circuit.
