Advertisements
Advertisements
Question
A source of ac voltage v = v0 sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
Solution

Using Kirchhoff’s loop rule in the above circuit,
\[V - L\frac{dI}{dt} = 0\]
\[\text { where, I is the instantaneous current flowing in the circuit }\]
\[ \Rightarrow L\frac{dI}{dt} = V_o \sin\omega t\]
\[ \Rightarrow \int dI = \frac{V_o}{L}\int\sin\omega tdt\]
\[ \Rightarrow I = \frac{V_o}{L}[ -\frac{\cos\omega t}{\omega}]\]
\[ \Rightarrow I = - \frac{V_o}{\omega L}\cos\omega t\]
\[ \Rightarrow I = \frac{V_o}{X_L}\sin(\omega t - \frac{\pi}{2})\]
\[\text { where, }X_L = \omega L = \text { inductance reactance }\]
\[ \therefore I = I_o \sin(\omega t - \frac{\pi}{2})\]
\[\text { where,} I_o = \frac{V_o}{X_L} =\text { peak value of ac}\]
\[\text { Now instantaneous power supplied by the source is } \]
\[P = VI = V_o I_o \sin\omega t \sin(\omega t - \frac{\pi}{2})\]
\[\text { Now the average power } ( P_{avg} ) \text { supplied over a complete cycle} ( 0 to 2\pi) \text { is }\]
\[ P_{avg} = \int_o^{2\pi} P = \int_o^{2\pi} V_o I_o \sin\theta \sin(\theta - \frac{\pi}{2})d\theta [\text { where } \theta = \omega t]\]
\[\text { Now over a complete cycle } \int_o^{2\pi} \sin\theta\sin(\theta - \frac{\pi}{2})d\theta = 0\]
\[\text { Therefore, }P_{avg} = \int_o^{2\pi} V_o I_o \text { sin }\theta\sin(\theta - \frac{\pi}{2})d\theta = 0\]
\[ P_{avg} = 0\]
Hence, the average power dissipated in the circuit is zero.
APPEARS IN
RELATED QUESTIONS
Show that in an a.c. circuit containing a pure inductor, the voltage is ahead of current by π/2 in phase ?
Find the value of t/τ for which the current in an LR circuit builds up to (a) 90%, (b) 99% and (c) 99.9% of the steady-state value.
A constant current exists in an inductor-coil connected to a battery. The coil is short-circuited and the battery is removed. Show that the charge flown through the coil after the short-circuiting is the same as that which flows in one time constant before the short-circuiting.
In a series, LCR circuit, obtain an expression for the resonant frequency,
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
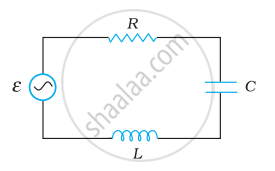
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
For a series LCR-circuit, the power loss at resonance is ______.
In series combination of R, L and C with an A.C. source at resonance, if R = 20 ohm, then impedence Z of the combination is ______.
Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
