Advertisements
Advertisements
Question
An inductor of inductance 2.00 H is joined in series with a resistor of resistance 200 Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) the current in the circuit, (b) the power delivered by the battery, (c) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
Solution
Given:-
Inductance of the inductor, L = 2 H
Resistance of the resistor connected to the inductor, R = 200 Ω,
Emf of the battery connected, E = 2 V
(a) The current in the LR circuit after t seconds after connecting the battery is given by
i = i0(1 − e−t/τ)
Here,
i0 = Steady state value of current
`i_0 = E/R=2/200A`
At time t = 10 ms, the current is given by
\[i= \frac{2}{200}(1 - e^{- 10 \times {10}^{- 3} \times 200/2} )\]
i = 0.01(1 − e−1)
i = 0.01(1 − 0.3678)
i = 0.01 × 0.632 = 6.3 mA
(b) The power delivered by the battery is given by
P = Vi
P = Ei0(1 − e−t/τ)
\[P = \frac{E^2}{R}(1 - e^{- t/\tau} )\]
\[P = \frac{2 \times 2}{200}(1 - e^{10 \times {10}^{- 3} \times 200/2} )\]
P = 0.02(1 − e−1)
P = 0.01264 = 12.6 mW
(c) The power dissipated in the resistor is given by
P1 = i2R
P1 = [i0(1 − e−t/τ)]2 R
P1 = (6.3 mA)2 × 200
P1 = 6.3 × 6.3 × 200 × 10−5
P1 = 79.38 × 10−4
P1 = 7.938 × 10−3 = 8 mW
(d) The rate at which the energy is stored in the magnetic field can be calculated as:-
\[W =\frac{1}{2}L i^2\]
\[W= \frac{L}{2} {i_0}^2 (1 - e^{- t/\tau} )^2\]
W = 2 × 10−2(0.225)
W = 0.455 × 10−2
W = 4.6 × 10−3
W = 4.6 mW
APPEARS IN
RELATED QUESTIONS
A series LCR circuit is connected across an a.c. source of variable angular frequency 'ω'. Plot a graph showing variation of current 'i' as a function of 'ω' for two resistances R1 and R2 (R1 > R2).
Answer the following questions using this graph :
(a) In which case is the resonance sharper and why?
(b) In which case in the power dissipation more and why?
A voltage V = V0 sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit?
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?
(ii) Without making any other change, find the value of the additional capacitor C1, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
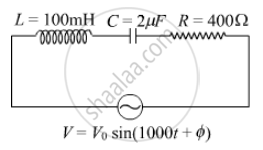
The figure shows a series LCR circuit with L = 10.0 H, C = 40 μF, R = 60 Ω connected to a variable frequency 240 V source, calculate
(i) the angular frequency of the source which drives the circuit at resonance,
(ii) the current at the resonating frequency,
(iii) the rms potential drop across the inductor at resonance.
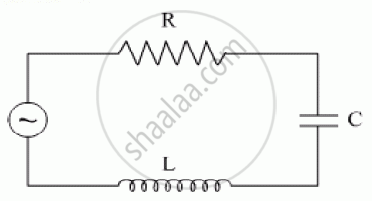
An LR circuit having a time constant of 50 ms is connected with an ideal battery of emf ε. find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and (c) the magnetic field energy stored in the circuit reaches half its maximum value.
A coil having an inductance L and a resistance R is connected to a battery of emf ε. Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value to half of the steady-state value.
An LR circuit with emf ε is connected at t = 0. (a) Find the charge Q which flows through the battery during 0 to t. (b) Calculate the work done by the battery during this period. (c) Find the heat developed during this period. (d) Find the magnetic field energy stored in the circuit at time t. (e) Verify that the results in the three parts above are consistent with energy conservation.
A constant current exists in an inductor-coil connected to a battery. The coil is short-circuited and the battery is removed. Show that the charge flown through the coil after the short-circuiting is the same as that which flows in one time constant before the short-circuiting.
Using the phasor diagram, derive the expression for the current flowing in an ideal inductor connected to an a.c. source of voltage, v= vo sin ωt. Hence plot graphs showing the variation of (i) applied voltage and (ii) the current as a function of ωt.
Choose the correct answer from given options
The selectivity of a series LCR a.c. circuit is large, when
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
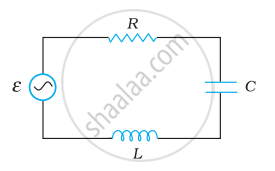
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
In a series LCR circuit supplied with AC, ______.
In an L.C.R. series a.c. circuit, the current ______.
A coil of 40 henry inductance is connected in series with a resistance of 8 ohm and the combination is joined to the terminals of a 2 volt battery. The time constant of the circuit is ______.
In a series LCR circuit the voltage across an inductor, capacitor and resistor are 20 V, 20 V and 40 V respectively. The phase difference between the applied voltage and the current in the circuit is ______.
In series LCR AC-circuit, the phase angle between current and voltage is
A series LCR circuit containing a 5.0 H inductor, 80 µF capacitors, and 40 Ω resistor is connected to a 230 V variable frequency ac source. The angular frequencies of the source at which power is transferred to the circuit are half the power at the resonant angular frequency are likely to be ______.
Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
A series LCR circuit driven by 300 V at a frequency of 50 Hz contains a resistance R = 3 kΩ, an inductor of inductive reactance XL = 250 πΩ, and an unknown capacitor. The value of capacitance to maximize the average power should be ______.
