Advertisements
Advertisements
Question
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
Solution
v = vm sin ωt
Let the current in the circuit be led the applied voltage by an angleΦ.
`i= i_m sin(omegat +phi)`
The Kirchhoff’s voltage law gives`L ((di)/dt +Ri +q/C = v)`.
It is given that v = vm sin ωt (applied voltage)
`L(d^2q)/(dt^2) +R(dq)/(dt) +q/C = v_m sinomegat ...... (1)`
On solving the equation, we obtain
`q = q_m sin(omegat + theta)`
`(dp)/(dt) = q_momega cos(omegat +theta)`
`((d^2)q)/(dt^2) = -q_momega^2 sin(omegat +theta)`
On substituting these values in equation (1), we obtain
`q_momega[R cos(omegat +theta)+ (X_c -X_L)sin(omegat +theta)] = v_msinomegat`
`X_c = 1/(omegaC) X_c = omegaL`
`Z = sqrt(R^2 +(X_c - X_L)^2`
`q_momegaZ[R/Z cos(omegat+theta)+((X_c -X_L))/Z sin (omegat+theta)] = v_m sin omegat ........... (2)`
Let `cos phi = R/2` and `(X_c -X_L)/Z = sinphi`
This gives
`tan phi = (X_c - X_L)/R`
On substituting this in equation (2), we obtain
`q_momegaZcos (omegat +theta -phi) = v_msinomegat`
On comparing the two sides, we obtain
`V_m = q_momegaZ = i+mZ`
`i_m = q_momega`
and `(theta-phi) = -pi/2`
`I = (dp)/(dt ) =q_momega cos (omegat+theta)`
`=i_m cos(omegat+theta)`
Or
`i = i_m sin(omegat +theta)`
Where,`i_m = (v_m)/Z = (v_m)/(sqrt(R^2 +(X_c - X_L)^2)`
And
`phi = tan^-1((X_c -X_L)/R)`
The condition for resonance to occur
`i_m = v_m/sqrt(R^2 +(X_C - X_L)^2)`
For resonance to occur, the value of im has to be the maximum.
The value of im will be the maximum when
`X_c = X_L`
`1/(omega C) = omegaL`
`omega^2 = 1/(LC)`
`omega = 1/(sqrtLC)`
`2pif = 1/sqrt(LC)`
`f = 1/(02pisqrt(LC)`
Power factor = cos Φ
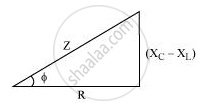
Where,`cosphi = R/Z = R/(sqrt(R^2 +(X_c- X_L)^2)`
(i) Conditions for maximum power factor (i.e., cos Φ = 1)
-
XC = XL
Or
-
R = 0
(ii) Conditions for minimum power factor
-
When the circuit is purely inductive
-
When the circuit is purely capacitive
APPEARS IN
RELATED QUESTIONS
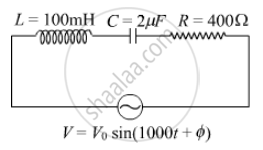
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?
(ii) Without making any other change, find the value of the additional capacitor C1, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
A series LCR circuit is connected to an ac source. Using the phasor diagram, derive the expression for the impedance of the circuit. Plot a graph to show the variation of current with frequency of the source, explaining the nature of its variation.
An L-R circuit has L = 1.0 H and R = 20 Ω. It is connected across an emf of 2.0 V at t = 0. Find di/dt at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1.0 s.
An inductor-coil of inductance 17 mH is constructed from a copper wire of length 100 m and cross-sectional area 1 mm2. Calculate the time constant of the circuit if this inductor is joined across an ideal battery. The resistivity of copper = 1.7 × 10−8 Ω-m.
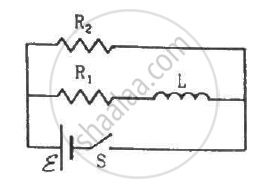
Consider the circuit shown in figure. (a) Find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c) Find the current through the inductor after one time constant.
In a series LCR circuit the voltage across an inductor, capacitor and resistor are 20 V, 20 V and 40 V respectively. The phase difference between the applied voltage and the current in the circuit is ______.
A series LCR circuit contains inductance 5 mH, capacitance 2µF and resistance ion. If a frequency A.C. source is varied, what is the frequency at which maximum power is dissipated?
The resonant frequency of a RF oscillator is 1 MHz and its bandwidth is 10 kHz. The quality factor will be :
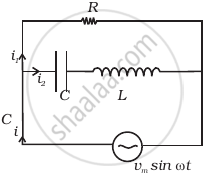
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
A series LCR circuit driven by 300 V at a frequency of 50 Hz contains a resistance R = 3 kΩ, an inductor of inductive reactance XL = 250 πΩ, and an unknown capacitor. The value of capacitance to maximize the average power should be ______.
