Advertisements
Advertisements
प्रश्न
In a series, LCR circuit, obtain an expression for the resonant frequency,
उत्तर
In a series LCR circuit,
`I=E/sqrt(R^2+(ωL-1/(ωc))^2`
From this equation, we may observe that when ω=0, I become O, and again when
ω = ∞, I = 0
∴ This implies there must be a value of ω at which I is maximum.
So when I is maximum, `sqrt(R^2+(ωL-1/(ωc))^2` is minimum
For this either R = 0, or ωL -` 1/(ωc) =0`
So when ωL -`1/(ωc)=0`, this is called resonance condition.
∴ At resonance,
ωL`=1/(ωc)`
⇒ `ω^2 =1/(Lc)`
⇒ `ω_r = 1/sqrt(Lc)`
⇒ `2pif_r = 1/sqrt(Lc)`
∴ `f_r` = Frequency of resonance
`=1/(2pi). 1/sqrt(Lc)`
i.e., `f_r =1/(2pi) . 1/sqrt(Lc)`
This is the required experssion for resonant frequency.
APPEARS IN
संबंधित प्रश्न
In a series LCR circuit, obtain the condition under which watt-less current flows in the circuit ?
The magnetic field at a point inside a 2.0 mH inductor-coil becomes 0.80 of its maximum value in 20 µs when the inductor is joined to a battery. Find the resistance of the circuit.
The current in a discharging LR circuit without the battery drops from 2.0 A to 1.0 A in 0.10 s. (a) Find the time constant of the circuit. (b) If the inductance of the circuit 4.0 H, what is its resistance?
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Using the phasor diagram, derive the expression for the current flowing in an ideal inductor connected to an a.c. source of voltage, v= vo sin ωt. Hence plot graphs showing the variation of (i) applied voltage and (ii) the current as a function of ωt.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
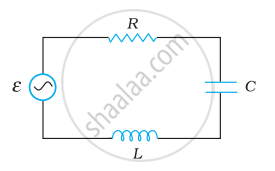
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
In a series LCR circuit supplied with AC, ______.
In an L.C.R. series a.c. circuit, the current ______.
Define Impedance.
A series RL circuit with R = 10 Ω and L = `(100/pi)` mH is connected to an ac source of voltage V = 141 sin (100 πt), where V is in volts and t is in seconds. Calculate
- the impedance of the circuit
- phase angle, and
- the voltage drop across the inductor.
