Advertisements
Advertisements
प्रश्न
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
उत्तर
Consider the LCR circuit
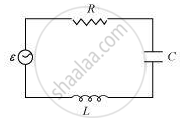
An AC source E with voltage `ν = ν_m` sin ωt is applied across LCR circuit
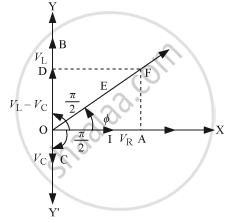
As the inductor, capacitor, and the resistor are connected in series so the current through all of them is the same (same amplitude and same phase)
Let the current be 1= Im sin wt
The voltage across each component has a different phase relation with the current.
- Let the maximum voltage across the resistor be VR = ImR that is in the same phase of the current hence it is represented by OA in the phasor diagram.
- Let the maximum voltage across the inductor be VL = ImXL and that leads the current by `pi/2` it is represented by OD in the phasor diagram.
- Let the maximum voltage across the capacitor be Vc = ImXc and that lags behind the current by `pi/2`, it is represented by OC in the phasor diagram.
Resultant voltage can be found by using the vector sum of the phasors. The resultant voltage is represented by OF.
It can be written as:
`V_m = sqrt(V_R^2 + (V_L - V_c)^2)`
`V_m = sqrt((I_mR)^2 + (I_mX_L - I_mX_c)^2)`
`V_m = I_m sqrt(R^2 + (X_L - X_c)^2)`
`Z = V_m/I_m = sqrt(R^2 + (X_L - X_c)^2)`
or, `Z = V_m/I_m = sqrt(R^2 + (ωL - 1/(ωC))^2)`
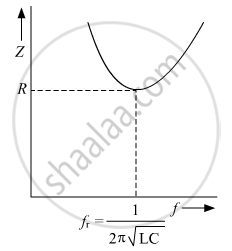
Variation of impedance Z with frequency f:
संबंधित प्रश्न
The figure shows a series LCR circuit with L = 10.0 H, C = 40 μF, R = 60 Ω connected to a variable frequency 240 V source, calculate
(i) the angular frequency of the source which drives the circuit at resonance,
(ii) the current at the resonating frequency,
(iii) the rms potential drop across the inductor at resonance.
An inductor-coil of resistance 10 Ω and inductance 120 mH is connected across a battery of emf 6 V and internal resistance 2 Ω. Find the charge which flows through the inductor in (a) 10 ms, (b) 20 ms and (c) 100 ms after the connections are made.
The magnetic field at a point inside a 2.0 mH inductor-coil becomes 0.80 of its maximum value in 20 µs when the inductor is joined to a battery. Find the resistance of the circuit.
An inductor of inductance 2.00 H is joined in series with a resistor of resistance 200 Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) the current in the circuit, (b) the power delivered by the battery, (c) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
Two coils A and B have inductances 1.0 H and 2.0 H respectively. The resistance of each coil is 10 Ω. Each coil is connected to an ideal battery of emf 2.0 V at t = 0. Let iA and iBbe the currents in the two circuit at time t. Find the ratio iA / iB at (a) t = 100 ms, (b) t = 200 ms and (c) t = 1 s.
Consider the circuit shown in figure. (a) Find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c) Find the current through the inductor after one time constant.
Figure shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 µF, R = 40 Ω.
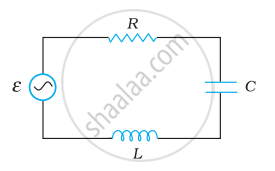
- Determine the source frequency which drives the circuit in resonance.
- Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
- Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
If the rms current in a 50 Hz ac circuit is 5 A, the value of the current 1/300 seconds after its value becomes zero is ______.
Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
