Advertisements
Advertisements
प्रश्न
A silver ball of radius 4.8 cm is suspended by a thread in a vacuum chamber. Ultraviolet light of wavelength 200 nm is incident on the ball for some time during which light energy of 1.0 × 10−7 J falls on the surface. Assuming that on average, one photon out of every ten thousand is able to eject a photoelectron, find the electric potential at the surface of the ball, assuming zero potential at infinity. What is the potential at the centre of the ball?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
उत्तर
Given:-
Radius of the silver ball, r = 4.8 cm
Wavelength of the ultra violet light, λ = 200 nm = 2 × 10−7 m
Total energy of light, E = 1.0 × 10−7 J
We are given that one photon out of every ten thousand is able to eject a photoelectron.
Energy of one photon,
`E^' = (hc)/lambda`,
where h = Planck's constant
c = speed of light
`lambda` = wavelength of light
On substituting the respective values in the above formula, we get :
`E^' = (6.63 xx 10^-34 xx 3 xx 10^8)/(2 xx 10^-7)`
`=9.945 xx 10^-19`
Number of photons,
`n = E/E^' = (1 xx 10^-7)/(9.945 xx 10^-19) = 1 xx 10^11`
Number of photoelectrons
= `(1 xx 10^11)/10^4 = 1 xx 10^7`
The amount of positive charge developed due to the outgoing electrons,
`q = 1 xx 10^7 xx 1.6 xx 10^-19`
`= 1.6 xx 10^-12 C`
Potential developed at the centre as well as on surface,
`V = (Kq)/r`,
where K = `1/(4piε_0)`
`therefore V = (9 xx 10^9 xx 1.6 xx 10^-12)/(4.8 xx 10^-2) = 0.3 V`
Potential inside the silver ball remains constant. Therefore, potential at the centre of the sphere is 0.3 V.
APPEARS IN
संबंधित प्रश्न
The threshold frequency for a certain metal is 3.3 × 1014 Hz. If light of frequency 8.2 × 1014 Hz is incident on the metal, predict the cutoff voltage for the photoelectric emission.
Light of frequency 7.21 × 1014 Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 105 m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons?
(a) A monoenergetic electron beam with electron speed of 5.20 × 106 m s−1 is subject to a magnetic field of 1.30 × 10−4 T normal to the beam velocity. What is the a radius of the circle traced by the beam, given e/m for electron equals 1.76 × 1011 C kg−1?
(b) Is the formula you employ in (a) valid for calculating the radius of the path of a 20 MeV electron beam? If not, in what way is it modified?
Is the formula you employ in (a) valid for calculating radius of the path of a 20 MeV electron beam? If not, in what way is it modified?
An electron gun with its collector at a potential of 100 V fires out electrons in a spherical bulb containing hydrogen gas at low pressure (∼10−2 mm of Hg). A magnetic field of 2.83 × 10−4 T curves the path of the electrons in a circular orbit of radius 12.0 cm. (The path can be viewed because the gas ions in the path focus the beam by attracting electrons, and emitting light by electron capture; this method is known as the ‘fine beam tube’ method. Determine e/m from the data.
If light of wavelength 412.5 nm is incident on each of the metals given below, which ones will show photoelectric emission and why?
| Metal | Work Function (eV) |
| Na | 1.92 |
| K | 2.15 |
| Ca | 3.20 |
| Mo | 4.17 |
Define the term "cut off frequency" in photoelectric emission. The threshod frequency of a metal is f. When the light of frequency 2f is incident on the metal plate, the maximum velocity of photo-electrons is v1. When the frequency of the incident radiation is increased to 5f, the maximum velocity of phto-electrons is v2. Find the ratio v1 : v2.
A photographic film is coated with a silver bromide layer. When light falls on this film, silver bromide molecules dissociate and the film records the light there. A minimum of 0.6 eV is needed to dissociate a silver bromide molecule. Find the maximum wavelength of light that can be recorded by the film.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A light beam of wavelength 400 nm is incident on a metal plate of work function 2.2 eV. (a) A particular electron absorbs a photon and makes two collisions before coming out of the metal. Assuming that 10% of the extra energy is lost to the metal in each collision, find the kinetic energy of this electron as it comes out of the metal. (b) Under the same assumptions, find the maximum number of collisions the electron can suffer before it becomes unable to come out of the metal.
A horizontal cesium plate (φ = 1.9 eV) is moved vertically downward at a constant speed v in a room full of radiation of wavelength 250 nm and above. What should be the minimum value of v so that the vertically-upward component of velocity is non-positive for each photoelectron?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
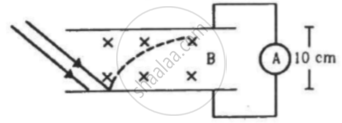
In an experiment on photoelectric effect, the emitter and the collector plates are placed at a separation of 10 cm and are connected through an ammeter without any cell. A magnetic field B exists parallel to the plates. The work function of the emitter is 2.39 eV and the light incident on it has wavelengths between 400 nm and 600 nm. Find the minimum value of B for which the current registered by the ammeter is zero. Neglect any effect of space charge.
Work function of aluminium is 4.2 eV. If two photons each of energy 2.5 eV are incident on its surface, will the emission of electrons take place? Justify your answer.
The stopping potential in an experiment on photoelectric effect is 1.5V. What is the maximum kinetic energy of the photoelectrons emitted? Calculate in Joules.
In the case of a photo electric effect experiment, explain the following facts, giving reasons.
The wave theory of light could not explain the existence of the threshold frequency.
In Photoelectric effect ______.
In the experimental set up for studying photoelectric effect, if keeping the frequency of the incident radiation and the accelerating potential fixed, the intensity of light is varied, then ______.
When a beam of 10.6 eV photons of intensity 2.0 W/m2 falls on a platinum surface of area 1.0 × 10-4 m2, only 53% of the incident photons eject photoelectrons. The number of photoelectrons emitted per second is ______.
An increase in the intensity of the radiation causing photo-electric emission from a surface does not affect the maximum K.E. of the photoelectrons. Explain.
