Advertisements
Advertisements
प्रश्न
(a) A monoenergetic electron beam with electron speed of 5.20 × 106 m s−1 is subject to a magnetic field of 1.30 × 10−4 T normal to the beam velocity. What is the a radius of the circle traced by the beam, given e/m for electron equals 1.76 × 1011 C kg−1?
(b) Is the formula you employ in (a) valid for calculating the radius of the path of a 20 MeV electron beam? If not, in what way is it modified?
उत्तर
(a) Speed of an electron, v = 5.20 × 106 m/s
Magnetic field experienced by the electron, B = 1.30 × 10−4 T
Specific charge of an electron, e/m = 1.76 × 1011 C kg−1
Where,
e = Charge on the electron = 1.6 × 10−19 C
m = Mass of the electron = 9.1 × 10−31 kg−1
The force exerted on the electron is given as:
`"F" = "e"|vec"v" xx vec"B"|`
= evB sin θ
θ = Angle between the magnetic field and the beam velocity
The magnetic field is normal to the direction of beam.
∴ θ = 90°
F = evB .............(1)
The beam traces a circular path of radius, r. It is the magnetic field, due to its bending nature, that provides the centripetal force `("F" = ("mv"^2)/"r")` for the beam.
Hence, equation (1) reduces to:
`"evB" = ("mv"^2)/"r"`
∴ r = `"mv"/("eB") = "v"/(("e"/"m")"B")`
= `(5.20 xx 10^6) /((1.76 xx 10^11) xx 1.30 xx 10^(-4))`
= 0.227 m
= 22.7 cm
Therefore, the radius of the circular path is 22.7 cm.
(b) Energy of the electron beam, E = 20 MeV = 20 × 106 × 1.6 × 10−19 J
The energy of the electron is given as:
`"E" = 1/2 "mv"^2`
∴ v = `((2"E")/"m")^(1/2)`
= `sqrt((2xx20xx10^6xx 1.6 xx 10^(-19))/(9.1 xx 10^(-31)))`
= 2.652 × 109 m/s
This result is incorrect because nothing can move faster than light. In the above formula, the expression (mv2/2) for energy can only be used in the non-relativistic limit, i.e., for v << c.
When very high speeds are concerned, the relativistic domain comes into consideration.
In the relativistic domain, mass is given as:
`"m" = "m"_0 [1 - "v"^2/"c"^2]^(1/2)`
Where,
`"m"_0` = Mass of the particle at rest
Hence, the radius of the circular path is given as:
r = `"mv"/"eB"`
= `("m"_0"v")/("eB"sqrt(("c"^2 - "v"^2)/"c"^2))`
APPEARS IN
संबंधित प्रश्न
The threshold frequency for a certain metal is 3.3 × 1014 Hz. If light of frequency 8.2 × 1014 Hz is incident on the metal, predict the cutoff voltage for the photoelectric emission.
Light of frequency 7.21 × 1014 Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 105 m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons?
What is so special about the combination e/m? Why do we not simply talk of e and m separately?
If light of wavelength 412.5 nm is incident on each of the metals given below, which ones will show photoelectric emission and why?
| Metal | Work Function (eV) |
| Na | 1.92 |
| K | 2.15 |
| Ca | 3.20 |
| Mo | 4.17 |
A light beam of wavelength 400 nm is incident on a metal plate of work function 2.2 eV. (a) A particular electron absorbs a photon and makes two collisions before coming out of the metal. Assuming that 10% of the extra energy is lost to the metal in each collision, find the kinetic energy of this electron as it comes out of the metal. (b) Under the same assumptions, find the maximum number of collisions the electron can suffer before it becomes unable to come out of the metal.
A horizontal cesium plate (φ = 1.9 eV) is moved vertically downward at a constant speed v in a room full of radiation of wavelength 250 nm and above. What should be the minimum value of v so that the vertically-upward component of velocity is non-positive for each photoelectron?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A silver ball of radius 4.8 cm is suspended by a thread in a vacuum chamber. Ultraviolet light of wavelength 200 nm is incident on the ball for some time during which light energy of 1.0 × 10−7 J falls on the surface. Assuming that on average, one photon out of every ten thousand is able to eject a photoelectron, find the electric potential at the surface of the ball, assuming zero potential at infinity. What is the potential at the centre of the ball?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Plot a graph to show the variation of stopping potential with frequency of incident radiation in relation to photoelectric effect.
Work function of aluminium is 4.2 eV. If two photons each of energy 2.5 eV are incident on its surface, will the emission of electrons take place? Justify your answer.
Answer the following question.
Why is the wave theory of electromagnetic radiation not able to explain the photoelectric effect? How does a photon picture resolve this problem?
In Photoelectric effect ______.
In the experimental set up for studying photoelectric effect, if keeping the frequency of the incident radiation and the accelerating potential fixed, the intensity of light is varied, then ______.
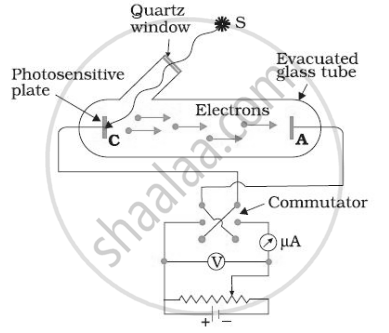
For a given frequency of light and a positive plate potential in the set up below, If the intensity of light is increased then ______.
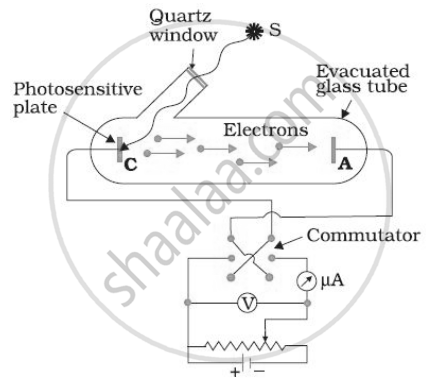
In various experiments on photo electricity, the stopping potential for a given frequency of the incident radiation is ______.
An increase in the intensity of the radiation causing photo-electric emission from a surface does not affect the maximum K.E. of the photoelectrons. Explain.
