Advertisements
Advertisements
प्रश्न
(a) A monoenergetic electron beam with electron speed of 5.20 × 106 m s−1 is subject to a magnetic field of 1.30 × 10−4 T normal to the beam velocity. What is the a radius of the circle traced by the beam, given e/m for electron equals 1.76 × 1011 C kg−1?
(b) Is the formula you employ in (a) valid for calculating the radius of the path of a 20 MeV electron beam? If not, in what way is it modified?
उत्तर
(a) Speed of an electron, v = 5.20 × 106 m/s
Magnetic field experienced by the electron, B = 1.30 × 10−4 T
Specific charge of an electron, e/m = 1.76 × 1011 C kg−1
Where,
e = Charge on the electron = 1.6 × 10−19 C
m = Mass of the electron = 9.1 × 10−31 kg−1
The force exerted on the electron is given as:
`"F" = "e"|vec"v" xx vec"B"|`
= evB sin θ
θ = Angle between the magnetic field and the beam velocity
The magnetic field is normal to the direction of beam.
∴ θ = 90°
F = evB .............(1)
The beam traces a circular path of radius, r. It is the magnetic field, due to its bending nature, that provides the centripetal force `("F" = ("mv"^2)/"r")` for the beam.
Hence, equation (1) reduces to:
`"evB" = ("mv"^2)/"r"`
∴ r = `"mv"/("eB") = "v"/(("e"/"m")"B")`
= `(5.20 xx 10^6) /((1.76 xx 10^11) xx 1.30 xx 10^(-4))`
= 0.227 m
= 22.7 cm
Therefore, the radius of the circular path is 22.7 cm.
(b) Energy of the electron beam, E = 20 MeV = 20 × 106 × 1.6 × 10−19 J
The energy of the electron is given as:
`"E" = 1/2 "mv"^2`
∴ v = `((2"E")/"m")^(1/2)`
= `sqrt((2xx20xx10^6xx 1.6 xx 10^(-19))/(9.1 xx 10^(-31)))`
= 2.652 × 109 m/s
This result is incorrect because nothing can move faster than light. In the above formula, the expression (mv2/2) for energy can only be used in the non-relativistic limit, i.e., for v << c.
When very high speeds are concerned, the relativistic domain comes into consideration.
In the relativistic domain, mass is given as:
`"m" = "m"_0 [1 - "v"^2/"c"^2]^(1/2)`
Where,
`"m"_0` = Mass of the particle at rest
Hence, the radius of the circular path is given as:
r = `"mv"/"eB"`
= `("m"_0"v")/("eB"sqrt(("c"^2 - "v"^2)/"c"^2))`
APPEARS IN
संबंधित प्रश्न
Is the formula you employ in (a) valid for calculating radius of the path of a 20 MeV electron beam? If not, in what way is it modified?
What is so special about the combination e/m? Why do we not simply talk of e and m separately?
Define the term "cut off frequency" in photoelectric emission. The threshod frequency of a metal is f. When the light of frequency 2f is incident on the metal plate, the maximum velocity of photo-electrons is v1. When the frequency of the incident radiation is increased to 5f, the maximum velocity of phto-electrons is v2. Find the ratio v1 : v2.
Visible light has wavelengths in the range of 400 nm to 780 nm. Calculate the range of energy of the photons of visible light.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In an experiment on photoelectric effect, light of wavelength 400 nm is incident on a cesium plate at the rate of 5.0 W. The potential of the collector plate is made sufficiently positive with respect to the emitter, so that the current reaches its saturation value. Assuming that on average, one out of every 106 photons is able to eject a photoelectron, find the photocurrent in the circuit.
In the arrangement shown in the figure, y = 1.0 mm, d = 0.24 mm and D = 1.2 m. The work function of the material of the emitter is 2.2 eV. Find the stopping potential V needed to stop the photocurrent.
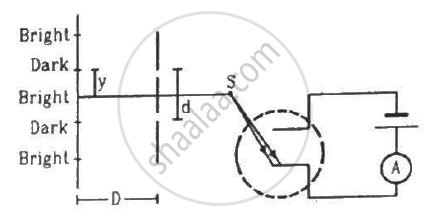
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Work function of aluminium is 4.2 eV. If two photons each of energy 2.5 eV are incident on its surface, will the emission of electrons take place? Justify your answer.
Answer the following question.
Why is the wave theory of electromagnetic radiation not able to explain the photoelectric effect? How does a photon picture resolve this problem?
In Photoelectric effect ______.
In the experimental set up for studying photoelectric effect, if keeping the frequency of the incident radiation and the accelerating potential fixed, the intensity of light is varied, then ______.
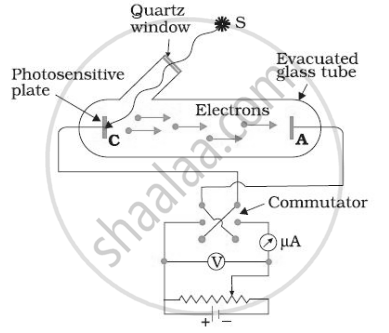
For a given frequency of light and a positive plate potential in the set up below, If the intensity of light is increased then ______.
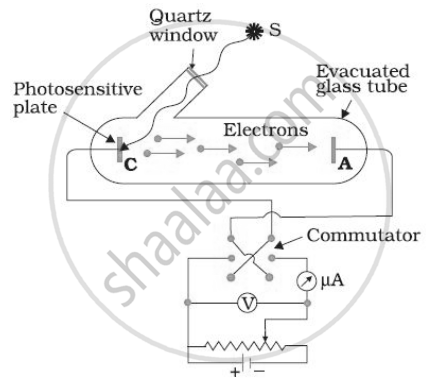
When a beam of 10.6 eV photons of intensity 2.0 W/m2 falls on a platinum surface of area 1.0 × 10-4 m2, only 53% of the incident photons eject photoelectrons. The number of photoelectrons emitted per second is ______.
The electromagnetic theory of light failed to explain ______.
Cathode rays can be deflected by
In photoelectric effect, the photoelectric current
