Advertisements
Advertisements
प्रश्न
A slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickness \[\frac{3d}{4}\]. Find the ratio of the capacitance with dielectric inside it to its capacitance without the dielectric.
उत्तर
\[\text { Capacitance of a capacitor without dielectric is given by }: \]
\[ C_o = \frac{\epsilon_o A}{d} . . . . . (i)\]
\[\text { Capacitance of capacitor when its plates are partly filled with dielectric of thickness t and of same area as the plates is given by }: \]
\[C = \frac{\epsilon_o A}{d - t (1 - \frac{1}{K})}\]
\[\text { Here} , t = \frac{3d}{4}\]
\[C = \frac{\epsilon_o A}{d - \frac{3d}{4}(1 - \frac{1}{K})} = \frac{\epsilon_o A}{\frac{dK + 3d}{4K}} = \frac{\epsilon_o A(4K)}{dK + 3d}\]
\[ = \frac{\epsilon_o A(4K)}{d(K + 3)} = \frac{4K}{(K + 3)} \times \frac{\epsilon_o A}{d}\]
\[\text { Therefore, the ratio of the capacitance with dielectric inside it to its capacitance without the dielectric is }\]
\[\frac{C_o}{C} = \frac{\frac{4K}{(K + 3)} \times \frac{\epsilon_o A}{d}}{\frac{\epsilon_o A}{d}} = \frac{4K}{(K + 3)}\]
APPEARS IN
संबंधित प्रश्न
Considering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law to include the term due to displacement current.
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to `(1/2)` QE, where Q is the charge on the capacitor, and E is the magnitude of the electric field between the plates. Explain the origin of the factor `1/2`.
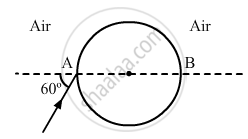
A ray of light falls on a transparent sphere with centre C as shown in the figure. The ray emerges from the sphere parallel to the line AB. Find the angle of refraction at A if the refractive index of the material of the sphere is \[\sqrt{3}\].
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
Define the capacitance of a capacitor and its SI unit.
A parallel-plate capacitor of plate area 40 cm2 and separation between the plates 0.10 mm, is connected to a battery of emf 2.0 V through a 16 Ω resistor. Find the electric field in the capacitor 10 ns after the connections are made.
A parallel-plate capacitor is filled with a dielectric material of resistivity ρ and dielectric constant K. The capacitor is charged and disconnected from the charging source. The capacitor is slowly discharged through the dielectric. Show that the time constant of the discharge is independent of all geometrical parameters like the plate area or separation between the plates. Find this time constant.
Answer the following question.
Describe briefly the process of transferring the charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
For a one dimensional electric field, the correct relation of E and potential V is _________.
In a parallel plate capacitor, the capacity increases if ______.
