Advertisements
Advertisements
प्रश्न
A transverse wave described by \[y = \left( 0 \cdot 02 m \right) \sin \left( 1 \cdot 0 m^{- 1} \right) x + \left( 30 s^{- 1} \right)t\] propagates on a stretched string having a linear mass density of \[1 \cdot 2 \times {10}^{- 4} kg m^{- 1}\] the tension in the string.
उत्तर
Given,
Wave equation,
\[y = \left( 0 \cdot 02 m \right)\sin\left( 1 \cdot 0 m^{- 1} \right)x + \left( 30 s^{- 1} \right)t\]
Let:
\[\text{ Mass per unit length, m = 1 . 2 \times {10}^{- 4} kg/m }\]
From the wave equation, we have:
\[k = 1 m^{- 1} = \frac{2\pi}{\lambda}\]
And,
\[\omega = 30 s^{- 1} = 2\pi f\]
Velocity of the wave in the stretched string is given by
\[\nu = \lambda f = \frac{\omega}{k} = \frac{30}{1}\]
\[ \Rightarrow v = 30 m/s\]
We know:
\[v = \sqrt{\frac{T}{m}}\]
\[ \Rightarrow 30 = \sqrt{\left( \frac{T}{1 . 2 \times {10}^{- 4}} \right)}\]
\[ \Rightarrow T = 108 \times {10}^{- 3} = 0 . 108 N\]
So, the tension in the string is 0.108 N.
APPEARS IN
संबंधित प्रश्न
When longitudinal wave is incident at the boundary of denser medium, then............................
- compression reflects as a compression.
- compression reflects as a rarefaction.
- rarefaction reflects as a compression.
- longitudinal wave reflects as transverse wave.
A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = cos x sin t + cos 2x sin 2t
Explain why (or how): Bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,
Explain why (or how) The shape of a pulse gets distorted during propagation in a dispersive medium.
A mechanical wave propagates in a medium along the X-axis. The particles of the medium
(a) must move on the X-axis
(b) must move on the Y-axis
(c) may move on the X-axis
(d) may move on the Y-axis.
A transverse wave travels along the Z-axis. The particles of the medium must move
Two wires of different densities but same area of cross section are soldered together at one end and are stretched to a tension T. The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
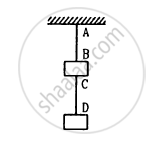
Two blocks each having a mass of 3⋅2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB (See following figure). The linear mass density of the wire AB is 10 g m−1 and that of CD is 8 g m−1. Find the speed of a transverse wave pulse produced in AB and CD.
An organ pipe, open at both ends, contains
A circular loop of string rotates about its axis on a frictionless horizontal place at a uniform rate so that the tangential speed of any particle of the string is ν. If a small transverse disturbance is produced at a point of the loop, with what speed (relative to the string) will this disturbance travel on the string?
A heavy but uniform rope of length L is suspended from a ceiling. (a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end. (b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach the ceiling? (c) A particle is dropped from the ceiling at the instant the bottom end is given the jerk. Where will the particle meet the pulse?
A tuning fork of frequency 440 Hz is attached to a long string of linear mass density 0⋅01 kg m−1 kept under a tension of 49 N. The fork produces transverse waves of amplitude 0⋅50 mm on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string?
If the speed of a transverse wave on a stretched string of length 1 m is 60 m−1, what is the fundamental frequency of vibration?
A steel wire of mass 4⋅0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
The equation of a standing wave, produced on a string fixed at both ends, is
\[y = \left( 0 \cdot 4 cm \right) \sin \left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
What could be the smallest length of the string?
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = 2 cos (3x) sin (10t)
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)
