Advertisements
Advertisements
प्रश्न
The equation of a standing wave, produced on a string fixed at both ends, is
\[y = \left( 0 \cdot 4 cm \right) \sin \left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
What could be the smallest length of the string?
उत्तर
Given:
Equation of the standing wave:
\[y = \left( 0 . 4 cm \right) \sin \left[ \left( 0 . 314 {cm}^{- 1} \right) x \right]\cos \left[ \left( 600 \pi s^{- 1} \right) t \right]\]
\[ \Rightarrow k = 0 . 314 = \frac{\pi}{10}\]
\[Also, k = \frac{2\pi}{\lambda}\]
\[ \Rightarrow \lambda = 20 \text{ cm }\]
We know:
\[L = \frac{n\lambda}{2}\]
For the smallest length, putting n = 1:
\[\Rightarrow L = \frac{\lambda}{2} = \frac{20 \text{ cm}}{2} = 10 \text{ cm }\]
Therefore, the required length of the string is 10 cm.
APPEARS IN
संबंधित प्रश्न
When longitudinal wave is incident at the boundary of denser medium, then............................
- compression reflects as a compression.
- compression reflects as a rarefaction.
- rarefaction reflects as a compression.
- longitudinal wave reflects as transverse wave.
When a transverse wave on a string is reflected from the free end, the phase change produced is ..............
(a) zero rad
(b) ` pi/2 ` rad
(c) `(3pi)/4` rad
(d) `pi` rad
A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36 t + 0.018 x + π/4)
Where x and y are in cm and t in s. The positive direction of x is from left to right.
(a) Is this a travelling wave or a stationary wave?
If it is travelling, what are the speed and direction of its propagation?
(b) What are its amplitude and frequency?
(c) What is the initial phase at the origin?
(d) What is the least distance between two successive crests in the wave?
Explain why (or how): Bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,
Explain why (or how) Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases
Explain why (or how) The shape of a pulse gets distorted during propagation in a dispersive medium.
Explain the reflection of transverse and longitudinal waves from a denser medium and a rared medium.
A mechanical wave propagates in a medium along the X-axis. The particles of the medium
(a) must move on the X-axis
(b) must move on the Y-axis
(c) may move on the X-axis
(d) may move on the Y-axis.
Mark out the correct options.
A steel wire of length 64 cm weighs 5 g. If it is stretched by a force of 8 N, what would be the speed of a transverse wave passing on it?
A vertical rod is hit at one end. What kind of wave propagates in the rod if (a) the hit is made vertically (b) the hit is made horizontally?
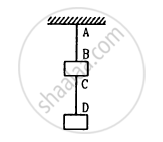
Two blocks each having a mass of 3⋅2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB (See following figure). The linear mass density of the wire AB is 10 g m−1 and that of CD is 8 g m−1. Find the speed of a transverse wave pulse produced in AB and CD.
An organ pipe, open at both ends, contains
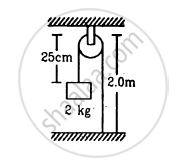
In the arrangement shown in figure , the string has a mass of 4⋅5 g. How much time will it take for a transverse disturbance produced at the floor to reach the pulley? Take g = 10 m s−2.
A steel wire of mass 4⋅0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
A wire, fixed at both ends is seen to vibrate at a resonant frequency of 240 Hz and also at 320 Hz. (a) What could be the maximum value of the fundamental frequency? (b) If transverse waves can travel on this string at a speed of 40 m s−1, what is its length?
Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies? (c) Which overtones are these frequencies? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string?
